题目内容
18.已知抛物线x2=2py(p>0)的焦点为F,过点F且倾斜角为150°的直线l与抛物线在第一、二象限分别交于A,B两点,则$\frac{{|{BF}|}}{{|{AF}|}}$等于( )| A. | 3 | B. | $7+4\sqrt{3}$ | C. | $\frac{1}{3}$ | D. | $3+2\sqrt{2}$ |
分析 设直线l的方程为:x=-$\sqrt{3}$(y-$\frac{p}{2}$),代入抛物线方程,求得A和B坐标,由抛物线的焦点弦公式,即可求得$\frac{{|{BF}|}}{{|{AF}|}}$的值.
解答 解:设A(x1,y1),B(x2,y2),直线l的方程为:x=-$\sqrt{3}$(y-$\frac{p}{2}$)则:
$\left\{\begin{array}{l}{{x}^{2}=2py}\\{x=-\sqrt{3}(y-1)}\end{array}\right.$,消去x可得12y2-20py+3p2=0,
点A在第一象限,解得:y1=$\frac{p}{6}$,y2=$\frac{3p}{2}$,
∴$\frac{{|{BF}|}}{{|{AF}|}}$=$\frac{{y}_{2}+\frac{p}{2}}{{y}_{1}+\frac{p}{2}}$=$\frac{\frac{3p}{2}+\frac{p}{2}}{\frac{p}{6}+\frac{p}{2}}$=3,
故选A.
点评 本题考查抛物线的焦点弦公式,直线与抛物线位置关系,考查计算能力,属于中档题.

练习册系列答案
相关题目
8.已知全集U={1,2,3,4,5,6,7,8},A={2,3,5,6},B={1,3,4,6,7},M={x|x∈A,且x∉B},则M=( )
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |
6.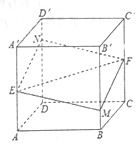 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:
(1)平面MENF⊥平面BDD′B′;
(2)当且仅当x=$\frac{1}{2}$时,四边形MENF的面积最小;
(3)四边形MENF周长L=f(x),x∈[0,1]是单调函数;
(4)四棱锥C′-MENF的体积V=h(x)为常函数,以上说法中正确的为( )
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:(1)平面MENF⊥平面BDD′B′;
(2)当且仅当x=$\frac{1}{2}$时,四边形MENF的面积最小;
(3)四边形MENF周长L=f(x),x∈[0,1]是单调函数;
(4)四棱锥C′-MENF的体积V=h(x)为常函数,以上说法中正确的为( )
| A. | (2)(3) | B. | (1)(3)(4) | C. | (1)(2)(3) | D. | (1)(2) |
13.已知命题p:“?x∈R,x2-x+2≥0”,则¬p是( )
| A. | ?x∉R,x2-x+2>0 | B. | ?x0∈R,x02-x0+2≤0 | ||
| C. | ?x0∈R,$x_0^2-{x_0}+2<0$ | D. | ?x0∉R,$x_0^2-{x_0}+2≤0$ |
8.下列函数中,在区间(1,+∞)上为增函数的是( )
| A. | y=x-1 | B. | $y={({\frac{1}{2}})^x}$ | C. | $y=\frac{1}{1-x}$ | D. | y=x2-4x |
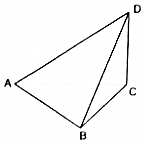 如图所示,在三棱锥D-ABC中,AB=BC=CD=2,AD=2$\sqrt{3}$,∠ABC=90°,平面ACD⊥平面ABC.
如图所示,在三棱锥D-ABC中,AB=BC=CD=2,AD=2$\sqrt{3}$,∠ABC=90°,平面ACD⊥平面ABC.