题目内容
16.设f(x)是定义在R上的偶函数,f(x)=-f(x+1),当x∈[0,1]时,f(x)=x+2,则当x∈[-2,0]时,f(x)=( )| A. | f(x)=x+4 | B. | f(x)=2+|x+1| | C. | f(x)=2-x | D. | f(x)=3-|x+1| |
分析 求出函数的周期,利用已知的函数的解析式求解所求的函数的解析式即可.
解答 解:f(x)是定义在R上的偶函数,f(x)=-f(x+1),
可得f(x+1)=-f(x),则f(x+2)=-f(x+1)=f(x),
函数的周期为:2,
当x∈[0,1]时,f(x)=x+2,当x∈[-1,0]时,f(x)=f(-x)=-x+2,
当x∈[-2,-1]时,x+2∈[0,1],f(x)=f(x+2)=x+4,
x∈[-1,0]时,-x∈[0,1],f(x)=f(-x)=-x+2,
即当x∈[-2,0]时,f(x)=3-|x+1|.
故选:D.
点评 本题主要考查抽象函数的应用,利用赋值法结合函数奇偶性和周期性的定义判断函数的性质是解决本题的关键.

练习册系列答案
相关题目
7.点P到直线y=3的距离比到点F(0,-1)的距离大2,则点P的轨迹方程为( )
| A. | y2=4x | B. | y2=-4x | C. | x2=4y | D. | x2=-4y |
11.已知幂函数f(x)=λ•xα的图象过点$P(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,则λ+α=( )
| A. | 2 | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
8.已知全集U={1,2,3,4,5,6,7,8},A={2,3,5,6},B={1,3,4,6,7},M={x|x∈A,且x∉B},则M=( )
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |
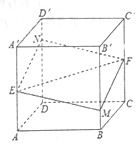 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法: