题目内容
16．函数$f（x）=lnx-\frac{2}{x}$的零点所在的大致区间是（ ）| A． | （e，+∞） | B． | $（\frac{1}{e}，1）$ | C． | （2，3） | D． | （e，+∞） |
分析 判断函数的单调性以及函数的连续性，利用零点判定定理推出结果即可．
解答 解：函数$f（x）=lnx-\frac{2}{x}$是单调增函数，也连续函数，
因为f（2）=ln2-1＜0，f（3）=ln3-$\frac{2}{3}$＞0，可得f（2）f（3）＜0，
所以函数的零点所在区间为（2，3）．
故选：C．
点评 本题考查函数的零点判定定理的应用，注意函数的单调性与连续性的判断．
练习册系列答案
相关题目
6．
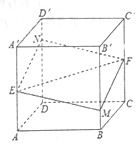如图所示，正方体ABCD-A′B′C′D′的棱长为1，E、F分别是棱是AA′，CC′的中点，过直线EF的平面分别与棱BB′，DD′交于M，N，设BM=x，x∈[0，1]，给出以下四种说法：
（1）平面MENF⊥平面BDD′B′；
（2）当且仅当x=$\frac{1}{2}$时，四边形MENF的面积最小；
（3）四边形MENF周长L=f（x），x∈[0，1]是单调函数；
（4）四棱锥C′-MENF的体积V=h（x）为常函数，以上说法中正确的为（ ）
如图所示，正方体ABCD-A′B′C′D′的棱长为1，E、F分别是棱是AA′，CC′的中点，过直线EF的平面分别与棱BB′，DD′交于M，N，设BM=x，x∈[0，1]，给出以下四种说法：（1）平面MENF⊥平面BDD′B′；
（2）当且仅当x=$\frac{1}{2}$时，四边形MENF的面积最小；
（3）四边形MENF周长L=f（x），x∈[0，1]是单调函数；
（4）四棱锥C′-MENF的体积V=h（x）为常函数，以上说法中正确的为（ ）
| A． | （2）（3） | B． | （1）（3）（4） | C． | （1）（2）（3） | D． | （1）（2） |
4．一个几何体的三视图如图所示，则该几何体的表面积为（ ）
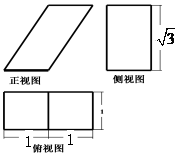
| A． | 2+4$\sqrt{3}$ | B． | 4+4$\sqrt{3}$ | C． | 8+2$\sqrt{3}$ | D． | 6+2$\sqrt{3}$ |
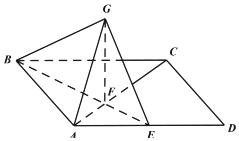如图，四边形 ABCD是平行四边形，AB=1，AD=2，AC=$\sqrt{3}$，E 是 AD的中点，BE与AC 交于点F，GF⊥平面ABCD．
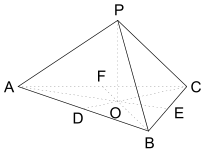ABC 是边长为6的等边三角形，P 为空间一点，PA=PB=PC，P到平面ABC距离为$\sqrt{3}$，则 PA与平面ABC 所成角的正弦值为$\frac{\sqrt{5}}{5}$．
8．下列函数中，在区间（1，+∞）上为增函数的是（ ）
| A． | y=x-1 | B． | $y={（{\frac{1}{2}}）^x}$ | C． | $y=\frac{1}{1-x}$ | D． | y=x2-4x |
5．如图，△A'O'B'为水平放置的△AOB的直观图，且O'A'=2，O'B'=3，则△AOB的周长为（ ）
| A． | 12 | B． | 10 | C． | 8 | D． | 7 |