题目内容
已知全集I={1，2，3，4，5}，集合A={1，2，3}，且A∩B={2，3}，则满足条件的B集合的个数为 ．
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：由全集I={1，2，3，4，5}，集合A={1，2，3}，且A∩B={2，3}可知，1∉B，2、3∈B，故只有4、5两个数可在或不在集合B中，由子集个数公式可得．
解答：
解：∵全集I={1，2，3，4，5}，集合A={1，2，3}，且A∩B={2，3}，
∴1∉B，2、3∈B，故只有4、5两个数可在或不在集合B中，
∴满足条件的B集合的个数为22=4．
故答案为：4．
∴1∉B，2、3∈B，故只有4、5两个数可在或不在集合B中，
∴满足条件的B集合的个数为22=4．
故答案为：4．
点评：本题考查了集合的运算与集合的子集个数的判断，属于基础题．
练习册系列答案
相关题目
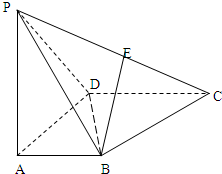四棱锥P-ABCD中，ABCD为平行四边形，PA⊥底面ABCD，∠BAC=30°，PA=BD，
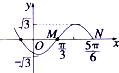已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象如图所示，若函数g（x）与函数f（x）的图象关于点P（
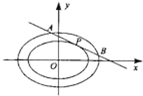已知椭圆E1：