题目内容
已知y=f(x)的定义域为[1,2].
(1)求f(2x+1)的定义域;
(2)求g(x)=f(1+x)+f(2-x)的定义域.
(1)求f(2x+1)的定义域;
(2)求g(x)=f(1+x)+f(2-x)的定义域.
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:(1)将2x+1代入f(x)的定义域,解出x即可;
(2)同样的将(1+x)与(2-x)分别代入f(x)的定义域解出方程组的解即可.
(2)同样的将(1+x)与(2-x)分别代入f(x)的定义域解出方程组的解即可.
解答:
解:(1)由1≤2x+1≤2得0≤x≤
,所以函数f(2x+1)的定义域是[0,
];
(2)由已知得
,解得0≤x≤1,所以g(x)=f(1+x)+f(2-x)的定义域为[0,1].
| 1 |
| 2 |
| 1 |
| 2 |
(2)由已知得
|
点评:本题考查了对函数定义域的理解,只要把握住“定义域就是自变量x的取值范围”则就能准确列出不等式组,注意最后结果写成集合或区间的形式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
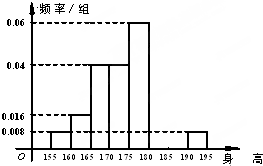 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.