题目内容
已知直线2x+y+4=0与x-y-1=0的交点为A,又已知点B(m,2),求直线AB的斜率,并指出直线AB的倾斜角的取值范围.
考点:直线的斜率,直线的倾斜角
专题:直线与圆
分析:联立方程组求解A的坐标,然后求出当m≠-1时直线AB的斜率,根据斜率不等于0求得直线AB的倾斜角的取值范围.
解答:
解:联立
,解得
,
∴A(-1,-2),
又B(m,2),
当m=-1时,直线AB的斜率不存在;
当m≠-1时,kAB=
=
.
∴直线AB的倾斜角的取值范围是(0°,180°).
|
|
∴A(-1,-2),
又B(m,2),
当m=-1时,直线AB的斜率不存在;
当m≠-1时,kAB=
| 2-(-2) |
| m-(-1) |
| 4 |
| m+1 |
∴直线AB的倾斜角的取值范围是(0°,180°).
点评:本题考查了直线的斜率,考查了直线的倾斜角和斜率的关系,是基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
设函数f(x)对于所有的正实数x均有f(3x)=3f(x),且f(x)=1-|x-2|(1≤x≤3),则使得f(x)=f(2014)的最小的正实数x的值为( )
| A、173 | B、416 |
| C、556 | D、589 |
直线2014x-y=0被圆x2+y2=1截得的弦长为( )
A、
| ||
| B、1 | ||
| C、4 | ||
| D、2 |
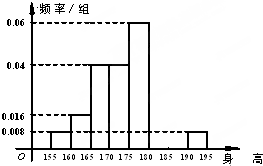 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.