题目内容
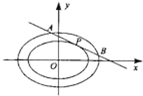已知椭圆E1：| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
（Ⅰ）已知x2+y2=r2上一点P（x0，y0），则过点P（x0，y0）的切线方程为xx0+yy0=r2．类比此结论，写出椭圆
| x2 |
| a2 |
| y2 |
| b2 |
（Ⅱ）求证：|AP|=|BP|．
考点：圆锥曲线的综合
专题：综合题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）切线方程
+
=1，利用导数法求斜率，即可得出结论；
（Ⅱ）
+
=1与
+
=2联立，利用韦达定理证明P为A，B中点，可得结论．
| x0x |
| a2 |
| y0y |
| b2 |
（Ⅱ）
| x0x |
| a2 |
| y0y |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
解答：
（Ⅰ）解：切线方程
+
=1
在第一象限内，由
+
=1可得y=
-------------（2分）
椭圆在点P处的切线斜率k=-
----------------（4分）
切线方程为y=-
（x-x0）+y0，即
+
=1．----------------（6分）
（Ⅱ）证明：设A（x1，y1），B（x2，y2），则
+
=1与
+
=2联立可得（b2+
）x2-
x+
-2a2b2=0---------------（9分）
所以
（x1+x2）=
•
=x0，
所以P为A，B中点，所以|AP|=|BP|．---------------（13分）
| x0x |
| a2 |
| y0y |
| b2 |
在第一象限内，由
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| a2-x2 |
椭圆在点P处的切线斜率k=-
| b2x0 |
| a2y0 |
切线方程为y=-
| b2x0 |
| a2y0 |
| x0x |
| a2 |
| y0y |
| b2 |
（Ⅱ）证明：设A（x1，y1），B（x2，y2），则
| x0x |
| a2 |
| y0y |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x02b4 |
| y02a2 |
| 2x0b4 |
| y02 |
| a2b4 |
| y02 |
所以
| 1 |
| 2 |
| 1 |
| 2 |
| ||
b2+
|
所以P为A，B中点，所以|AP|=|BP|．---------------（13分）
点评：本题考查：圆锥曲线的综合，考查导数知识，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目