题目内容
14.已知cos($\frac{π}{4}-\frac{θ}{2}$)=$\frac{2}{3}$,则sinθ=( )| A. | $\frac{7}{9}$ | B. | $\frac{1}{9}$ | C. | -$\frac{1}{9}$ | D. | -$\frac{7}{9}$ |
分析 利用二倍角的余弦公式、诱导公式,求得sinθ的值.
解答 解:∵cos($\frac{π}{4}-\frac{θ}{2}$)=$\frac{2}{3}$,∴cos($\frac{π}{2}$-θ)=2${cos}^{2}(\frac{π}{4}-\frac{θ}{2})$-1=-$\frac{1}{9}$=sinθ,
即sinθ=-$\frac{1}{9}$,
故选:C.
点评 本题主要考查二倍角的余弦公式、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
5.平面直角坐标系中,在直线x=1,y=1与坐标轴围成的正方形内任取一点,则此点落在曲线y=x2下方区域的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
19.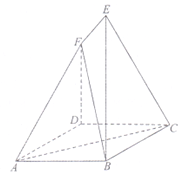 如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a
如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a
(Ⅰ)求证:EF丄AC;
(Ⅱ)求直线CE与平面ABF所成角的正弦值.
 如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a
如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a(Ⅰ)求证:EF丄AC;
(Ⅱ)求直线CE与平面ABF所成角的正弦值.
6.从区间[0,1]随机选取三个数x,y,z,若满足x2+y2+z2>1,则记参数t=1,否则t=0,在进行1000次重复试验后,累计所有参数的和为477,由此估算圆周率π的值应为( )
| A. | 3.084 | B. | 3.138 | C. | 3.142 | D. | 3.136 |
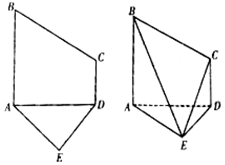 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.