题目内容
6．从区间[0，1]随机选取三个数x，y，z，若满足x2+y2+z2＞1，则记参数t=1，否则t=0，在进行1000次重复试验后，累计所有参数的和为477，由此估算圆周率π的值应为（ ）| A． | 3.084 | B． | 3.138 | C． | 3.142 | D． | 3.136 |
分析 由题意，$\frac{477}{1000}$=1-$\frac{1}{8}×\frac{4}{3}π×{1}^{3}$，即可计算圆周率π的值．
解答 解：由题意，$\frac{477}{1000}$=1-$\frac{1}{8}×\frac{4}{3}π×{1}^{3}$，∴π=3.138，
故选B．
点评 本题考查概率的计算，考查几何概型，比较基础．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
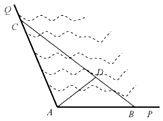如图所示，∠PAQ是某海湾旅游区的一角，其中∠PAQ=120°，为了营造更加优美的旅游环境，旅游区管委员会决定在直线海岸AP和AQ上分别修建观光长廊AB和AC，其中AB是宽长廊，造价是800元/米；AC是窄长廊，造价是400元/米；两段长廊的总造价为120万元，同时在线段BC上靠近点B的三等分点D处建一个观光平台，并建水上直线通道AD（平台大小忽略不计），水上通道的造价是1000元/米．
14．已知cos（$\frac{π}{4}-\frac{θ}{2}$）=$\frac{2}{3}$，则sinθ=（ ）
| A． | $\frac{7}{9}$ | B． | $\frac{1}{9}$ | C． | -$\frac{1}{9}$ | D． | -$\frac{7}{9}$ |
1．若集合M={y∈N|y＜6}，N={x|log2（x-1）≤2}，则M∩N=（ ）
| A． | （1，5] | B． | （-∞，5] | C． | {1，2，3，4，5} | D． | {2，3，4，5} |