题目内容
2.中国清朝数学家李善兰在1859年翻译《代数学》中首次将“function”译做:“函数”,沿用至今,为什么这么翻译,书中解释说“凡此变数中函彼变数者,则此为彼之函数”.1930年美国人给出了我们课本中所学的集合论的函数定义,已知集合M={-1,1,2,4},N={1,2,4,16},给出下列四个对应法则:①y=log2|x|,②y=x+1,③y=2|x|,④y=x2,请由函数定义判断,其中能构成从M到N的函数的是( )| A. | ①③ | B. | ①② | C. | ③④ | D. | ②④ |
分析 在①中,当x=±1时,y=log21=0∉N;在②中,当x=-1时,y=-1+1=0∉N;在③中,任取x∈M,总有y=2|x|∈N;在④中,任取x∈M,总有y=x2∈N.
解答 解:在①中,当x=±1时,y=log21=0∉N,故①错误;
在②中,当x=-1时,y=-1+1=0∉N,故②错误;
在③中,任取x∈M,总有y=2|x|∈N,故③正确;
在④中,任取x∈M,总有y=x2∈N,故④正确.
故选:C.
点评 本题考查函数的判断,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一条渐近线与直线x+y+1=0垂直,则该双曲线的焦距为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
14.已知cos($\frac{π}{4}-\frac{θ}{2}$)=$\frac{2}{3}$,则sinθ=( )
| A. | $\frac{7}{9}$ | B. | $\frac{1}{9}$ | C. | -$\frac{1}{9}$ | D. | -$\frac{7}{9}$ |
16. 如图,在直三棱柱ABC-A1B1C1中,AB=BC=2$\sqrt{2},C{C_1}$=4,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从点E到点F的最短路径的长度为( )
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2$\sqrt{2},C{C_1}$=4,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从点E到点F的最短路径的长度为( )
 如图,在直三棱柱ABC-A1B1C1中,AB=BC=2$\sqrt{2},C{C_1}$=4,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从点E到点F的最短路径的长度为( )
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2$\sqrt{2},C{C_1}$=4,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从点E到点F的最短路径的长度为( )| A. | $\sqrt{14+4\sqrt{2}}$ | B. | $\sqrt{22}$ | C. | $3\sqrt{2}$ | D. | $2\sqrt{3}$ |
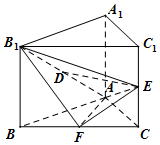 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.