题目内容
5.平面直角坐标系中,在直线x=1,y=1与坐标轴围成的正方形内任取一点,则此点落在曲线y=x2下方区域的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
分析 由题意,利用几何概型的公式可求.
解答 解:直线x=1,y=1与坐标轴围成的正方形面积为1,
在曲线y=x2下方区域的面积为:${∫}_{0}^{1}{x}^{2}dx=\frac{1}{3}{x}^{3}{|}_{0}^{1}=\frac{1}{3}$,
由几何概型的公式得到概率为$\frac{\frac{1}{3}}{1}=\frac{1}{3}$;
故选A.
点评 本题考查了几何概型的概率求法;关键是明确面积比为所求概率;同时考查利用定积分求曲边梯形的面积;注意掌握.

练习册系列答案
相关题目
15.为了了解某校学生喜欢吃零食是否与性别有关,随机对此校100人进行调查,得到如下的列表:已知在全部100人中随机抽取1人,抽到不喜欢吃零食的学生的概率为$\frac{2}{5}$.
(Ⅰ)请将上面的列表补充完整;
(Ⅱ)是否有99.9%以上的把握认为喜欢吃零食与性别有关?说明理由.下面的临界值表供参考:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
| 喜欢吃零食 | 不喜欢吃零食辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
(Ⅱ)是否有99.9%以上的把握认为喜欢吃零食与性别有关?说明理由.下面的临界值表供参考:
| p(K2≥k) | 0.010 | 0.005 | 0.001 |
| k | 6.635 | 7.879 | 10.828 |
14.已知cos($\frac{π}{4}-\frac{θ}{2}$)=$\frac{2}{3}$,则sinθ=( )
| A. | $\frac{7}{9}$ | B. | $\frac{1}{9}$ | C. | -$\frac{1}{9}$ | D. | -$\frac{7}{9}$ |
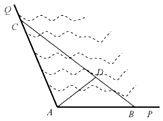 如图所示,∠PAQ是某海湾旅游区的一角,其中∠PAQ=120°,为了营造更加优美的旅游环境,旅游区管委员会决定在直线海岸AP和AQ上分别修建观光长廊AB和AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价为120万元,同时在线段BC上靠近点B的三等分点D处建一个观光平台,并建水上直线通道AD(平台大小忽略不计),水上通道的造价是1000元/米.
如图所示,∠PAQ是某海湾旅游区的一角,其中∠PAQ=120°,为了营造更加优美的旅游环境,旅游区管委员会决定在直线海岸AP和AQ上分别修建观光长廊AB和AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价为120万元,同时在线段BC上靠近点B的三等分点D处建一个观光平台,并建水上直线通道AD(平台大小忽略不计),水上通道的造价是1000元/米.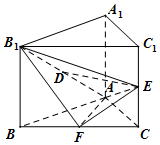 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.