题目内容
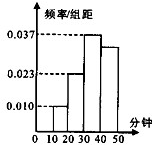 学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )
学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )| A、100 | B、120 |
| C、130 | D、390 |
考点:频率分布直方图
专题:概率与统计
分析:由频率分布直方图,求出每天课外阅读时间在[10,30)的频率,从而得出在[30,50)的频率,即可求出n的值.
解答:
解:由频率分布直方图得,每天课外阅读时间在[10,20)和[20,30)的频率分别为
0.010×(20-10)=0.10,
0.023×(30-20)=0.23;
∴每天课外阅读时间在[30,50)的频率为:
1-(0.10+0.23)=0.67,
∴抽取的学生数n=67÷0.67=100;
故选:A.
0.010×(20-10)=0.10,
0.023×(30-20)=0.23;
∴每天课外阅读时间在[30,50)的频率为:
1-(0.10+0.23)=0.67,
∴抽取的学生数n=67÷0.67=100;
故选:A.
点评:本题考查了频率分布直方图的应用问题,解题的关键是读懂图形,求出每天课外阅读时间在[30,50)的频率,是基础题.

练习册系列答案
相关题目
已知函数f(x)为奇函数,且当x>0时,f(x)=x2+2x,则f(-1)=( )
| A、1 | B、-1 | C、3 | D、-3 |
已知变量x,y满足约束条件
,则z=3x+2y的最大值为( )
|
| A、1 | B、13 | C、11 | D、-1 |
给出下列命题:
(1)两个具有公共终点的向量,一定是共线向量.
(2)两个向量不能比较大小,但它们的模能比较大小.
(3)λ
=0(λ为实数),则λ必为零.
(4)λ,μ为实数,若λ
=μ
,则
与
共线.
其中错误的命题的个数为( )
(1)两个具有公共终点的向量,一定是共线向量.
(2)两个向量不能比较大小,但它们的模能比较大小.
(3)λ
| a |
(4)λ,μ为实数,若λ
| a |
| b |
| a |
| b |
其中错误的命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
下列说法错误的是( )
| A、平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行 |
| B、一个平面内的两条相交直线与另外一个平面平行,则这两个平面平行 |
| C、一条直线与一个平面内的两条直线都垂直,则该直线与此平面垂直 |
| D、如果两个平行平面同时和第三个平面相交,则它们的交线平行 |
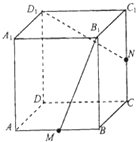 如图正方体中,M、N分别是棱AB、CC1的中点,
如图正方体中,M、N分别是棱AB、CC1的中点,