题目内容
P是圆O:x2+y2=4上的动点,过P作x轴的垂线,垂足为Q,若PQ中点M的轨迹记为Γ.
(1)求Γ的方程;
(2)若直线l:y=kx+3与曲线Γ相切,求直线l被圆O截得的弦长.
(1)求Γ的方程;
(2)若直线l:y=kx+3与曲线Γ相切,求直线l被圆O截得的弦长.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)设M(x,y)是轨迹Γ上一点,对应的圆O上的点为P(x0,y0),利用相关点法能求出曲线Γ方程.
(2)由
,得(1+4k2)x2+24kx+32=0,由此利用分类讨论思想能求出直线l被圆O截得的弦长.
(2)由
|
解答:
解:(1)设M(x,y)是轨迹Γ上任意一点,
对应的圆O上的点为P(x0,y0)…(1分),
则x02+y02=4…(2分),且
,即
,…(4分),
∴x 2+(2y)2=4…(5分),
即
+y2=1,
∴曲线Γ方程为
+y2=1…(6分).
(2)由
…(7分),
得(1+4k2)x2+24kx+32=0…(8分)
∵直线l与曲线Γ相切,
∴△=(24k)2-4(1+4k2)•32=0…(9分)
解得k2=2,则k=±
…(10分)
当k=
时,直线l:y=
x+3,
此时圆O的圆心到直线l的距离d=
=
…(12分),
直线l被圆O截得的弦长为2
=2…(13分)
当k=-
时,根据椭圆和圆的对称性知,直线l被圆O截得的弦长为2.…(14分).
对应的圆O上的点为P(x0,y0)…(1分),
则x02+y02=4…(2分),且
|
|
∴x 2+(2y)2=4…(5分),
即
| x2 |
| 4 |
∴曲线Γ方程为
| x2 |
| 4 |
(2)由
|
得(1+4k2)x2+24kx+32=0…(8分)
∵直线l与曲线Γ相切,
∴△=(24k)2-4(1+4k2)•32=0…(9分)
解得k2=2,则k=±
| 2 |
当k=
| 2 |
| 2 |
此时圆O的圆心到直线l的距离d=
| 3 | ||
|
| 3 |
直线l被圆O截得的弦长为2
| 4-3 |
当k=-
| 2 |
点评:本题考查椭圆方程的求法,考查直线被圆截得的弦长的求法,是中档题,解题时要注意分类讨论思想的合理运用.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
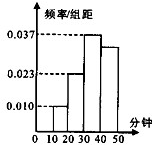 学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )
学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )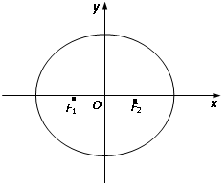 如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-
如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-