题目内容
已知变量x,y满足约束条件
,则z=3x+2y的最大值为( )
|
| A、1 | B、13 | C、11 | D、-1 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对于的平面区域,利用数形结合即可得到结论.
解答:
解:作出不等式组对于的平面区域如图:
由z=3x+2y,则y=-
x+
,
平移直线y=-
x+
,由图象可知当直线y=-
x+
,
经过点A时,直线y=-
x+
的截距最大,此时z最大,
由
,解得
,
即A(3,2),
此时zmax=3×3+2×2=13,
故选:B

由z=3x+2y,则y=-
| 3 |
| 2 |
| z |
| 2 |
平移直线y=-
| 3 |
| 2 |
| z |
| 2 |
| 3 |
| 2 |
| z |
| 2 |
经过点A时,直线y=-
| 3 |
| 2 |
| z |
| 2 |
由
|
|
即A(3,2),
此时zmax=3×3+2×2=13,
故选:B
点评:本题主要考查线性规划的应用,利用z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
已知变量x,y满足
,则xy的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
在下列四个选项中,说法错误的是( )
| A、若A是B的必要不充分条件,则非B也是非A的必要不充分条件 | |||||
B、“
| |||||
| C、“x≠1”是“x2≠1”的充分不必要条件 | |||||
| D、“x≠0”是“x+|x|>0”的必要不充分条件 |
下列命题中,真命题是( )
| A、存在一个△ABC,使a2=b2+c2-3bccosA(a,b,c是三边长,a是内角A的对边) |
| B、?x∈(1,+∞),log0.5x>0 |
| C、幂函数 f(x)=(m-1)xm-3在定义域上是减函数 |
| D、a>1,b>1是ab>1的必要条件 |
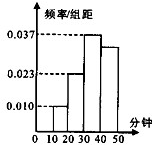 学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )
学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )