题目内容
下列四个命题正确的是( )
①函数y=x+
(x≠0)的值域是[1,+∞);
②平面内的动点P到点F(-2,3)和到直线l:2x+y+1=0的距离相等,则P的轨迹是抛物线;
③直线AB与平面α相交于点B,且AB与α内相交于点C的三条互不重合的直线CD、CE、CF所成的角相等,则AB⊥α;
④若f(x)=x2+bx+c(b,c∈R),则f(
)≤
[f(x1)+f(x2)].
①函数y=x+
| 1 |
| 4x |
②平面内的动点P到点F(-2,3)和到直线l:2x+y+1=0的距离相等,则P的轨迹是抛物线;
③直线AB与平面α相交于点B,且AB与α内相交于点C的三条互不重合的直线CD、CE、CF所成的角相等,则AB⊥α;
④若f(x)=x2+bx+c(b,c∈R),则f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
| A、①③ | B、②④ | C、②③ | D、③④ |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用基本不等式证明.②利用抛物线的定义判断.③利用线面垂直的判定定理或性质定理判断.④利用凸凹函数的性质判断.
解答:
解:①当x>0时,y=x+
≥2
=1,
当x<0时,y=x+
=-[(-x)+]≤
-2
=-1,
所以函数的值域是[1,+∞)∪(-∞,-1],所以①错误.
②因为点F(-2,3)在直线2x+y+1=0,所以点P的轨迹不是抛物线,是过点F且垂直于直线l的直线.所以②错误.
③若AB不垂直α,当AB与直线CB、CE、CF所成的角相等,则必有CB∥CE/CF,与直线CB、CE、CF互不重合,矛盾,
所以假设不成立,所以必有AB⊥α.所以③正确.
④因为满足f(
)≤
[f(x1)+f(x2)].的函数为凹函数,所以二次函数是凹函数,所以④正确.
故正确的命题的编号是③④.
故答案为:③④.
故选:D.
| 1 |
| 4x |
x•
|
当x<0时,y=x+
| 1 |
| 4x |
| 1 |
| -4x |
(-x)•(
|
所以函数的值域是[1,+∞)∪(-∞,-1],所以①错误.
②因为点F(-2,3)在直线2x+y+1=0,所以点P的轨迹不是抛物线,是过点F且垂直于直线l的直线.所以②错误.
③若AB不垂直α,当AB与直线CB、CE、CF所成的角相等,则必有CB∥CE/CF,与直线CB、CE、CF互不重合,矛盾,
所以假设不成立,所以必有AB⊥α.所以③正确.
④因为满足f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
故正确的命题的编号是③④.
故答案为:③④.
故选:D.
点评:本题主要考查了命题的真假判断,综合性较强.要求对相关知识要熟练理解和掌握.

练习册系列答案
相关题目
已知变量x,y满足
,则xy的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
下列命题中,真命题是( )
| A、存在一个△ABC,使a2=b2+c2-3bccosA(a,b,c是三边长,a是内角A的对边) |
| B、?x∈(1,+∞),log0.5x>0 |
| C、幂函数 f(x)=(m-1)xm-3在定义域上是减函数 |
| D、a>1,b>1是ab>1的必要条件 |
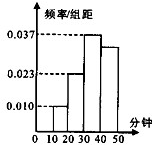 学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )
学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )| A、100 | B、120 |
| C、130 | D、390 |
若实数x,y满足
,则z=3x+2y的最大值是( )
|
| A、0 | ||
| B、1 | ||
C、
| ||
| D、9 |
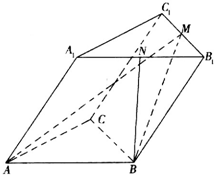 如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.
如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.