题目内容
若点A(1,2)是抛物线C:y2=2px(p>0)上一点,经过点B(5,-2)的直线l与抛物线C交于P,Q两点.
(Ⅰ)求证:
•
为定值;
(Ⅱ)若点P,Q与点A不重合,问△APQ的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
(Ⅰ)求证:
| PA |
| QA |
(Ⅱ)若点P,Q与点A不重合,问△APQ的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由已知条件求出抛物线C:y2=4x,若直线l的斜率不存在,直线l:x=5,
•
=0;若直线l的斜率存在,设直线l:y=k(x-5)-2,(k≠0),利用根的判别式和韦达定理能推导出
•
为定值0.
(II) 若直线l的斜率不存在,直线l:x=5,S△APQ=
×4
×4=8
;若直线l的斜率存在时,令u=(
+1)2,有u≥0,推导出S△APQ=8
没有最大值.
| PA |
| QA |
| PA |
| QA |
(II) 若直线l的斜率不存在,直线l:x=5,S△APQ=
| 1 |
| 2 |
| 5 |
| 5 |
| 1 |
| k |
| u2+4u |
解答:
解:(I)∵点A(1,2)在抛物线C:y2=2px(p>0)上,
∴4=2p,解得p=2,∴抛物线C:y2=4x,(2分)
若直线l的斜率不存在,直线l:x=5,
此时P(5,2
),Q(5,-2
),A(1,2),
∴
•
=(-4,2-2
)•(-4,2+2
)=0,(3分)
若直线l的斜率存在,设直线l:y=k(x-5)-2,(k≠0),
点P(x1,y1),Q(x2,y2)
联立
,
消去x,得ky2-4y-4(5k+2)=0,
∴y1+y2=
,y1y2=-
=-20-
,
△=16+16k(5k+2)>0,(5分)
∴
•
=(1-x1,3=2-y1)•(1-x2,2-y2)
=1-(x1+x2)+x1x2+4-2(y1+y2)+y1y2
=1-
+
+4-2(y1+y2)+y1y2
=1-
+
+4-2(y1+y2)+y1y2
=1-
+
+4-
-20-
=0,
∴
•
为定值0.(7分)
(II) 若直线l的斜率不存在,直线l:x=5,
此时P(5,2
),Q(5,-2
),A(1,2),
S△APQ=
×4
×4=8
若直线l的斜率存在时,
|PQ|=
=
•
=
•
,(9分)
点A(1,2)到直线l:y=k(x-5)-2的距离h=
,(10分)
S△APQ=
•|PQ|•h=8
,
令u=(
+1)2,有u≥0,
则S△APQ=8
没有最大值.(12分)
∴4=2p,解得p=2,∴抛物线C:y2=4x,(2分)
若直线l的斜率不存在,直线l:x=5,
此时P(5,2
| 5 |
| 5 |
∴
| PA |
| QA |
| 5 |
| 5 |
若直线l的斜率存在,设直线l:y=k(x-5)-2,(k≠0),
点P(x1,y1),Q(x2,y2)
联立
|
消去x,得ky2-4y-4(5k+2)=0,
∴y1+y2=
| 4 |
| k |
| 20k+8 |
| k |
| 8 |
| k |
△=16+16k(5k+2)>0,(5分)
∴
| PA |
| QA |
=1-(x1+x2)+x1x2+4-2(y1+y2)+y1y2
=1-
| y12+y22 |
| 4 |
| y12y22 |
| 16 |
=1-
| (y1+y2)2-2y1y2 |
| 4 |
| y12y22 |
| 16 |
=1-
| ||||
| 4 |
(-20-
| ||
| 16 |
| 8 |
| k |
| 8 |
| k |
∴
| PA |
| QA |
(II) 若直线l的斜率不存在,直线l:x=5,
此时P(5,2
| 5 |
| 5 |
S△APQ=
| 1 |
| 2 |
| 5 |
| 5 |
若直线l的斜率存在时,
|PQ|=
| (x1-x2)2+(y1-y2)2 |
=
1+
|
| (y1+y2)2-4y1y2 |
1+
|
|
点A(1,2)到直线l:y=k(x-5)-2的距离h=
| 4|k+1| | ||
|
S△APQ=
| 1 |
| 2 |
|
令u=(
| 1 |
| k |
则S△APQ=8
| u2+4u |
点评:本题考查两个向量的数量积为定理,考查三角形的面积是否有最大值的判断,解题时要认真审题,注意根的判别式和韦达定理的合理运用.

练习册系列答案
相关题目
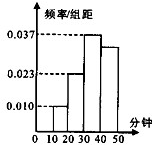 学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )
学校为了了解学生每天课外阅读的时问(单位:分钟),抽取了n个学生进行调查,结果显示这些学生的课外阅读时间都在[10,50),其频率分布直方图如图所示,其中时间在[30,50)的学生有67人,则n的值是( )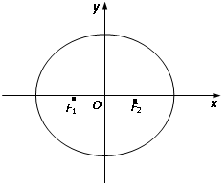 如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-
如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-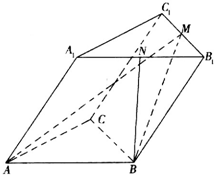 如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.
如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.