题目内容
给出下列命题：
（1）两个具有公共终点的向量，一定是共线向量．
（2）两个向量不能比较大小，但它们的模能比较大小．
（3）λ
=0（λ为实数），则λ必为零．
（4）λ，μ为实数，若λ
=μ
，则
与
共线．
其中错误的命题的个数为（ ）
（1）两个具有公共终点的向量，一定是共线向量．
（2）两个向量不能比较大小，但它们的模能比较大小．
（3）λ
| a |
（4）λ，μ为实数，若λ
| a |
| b |
| a |
| b |
其中错误的命题的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：命题的真假判断与应用
专题：平面向量及应用
分析：（1）利用共线向量的定义即可判断出；
（2）利用向量的定义即可判断出；
（3）利用向量的数乘即可得出；
（4）利用向量共线定理即可判断出．
（2）利用向量的定义即可判断出；
（3）利用向量的数乘即可得出；
（4）利用向量共线定理即可判断出．
解答：
解：（1）两个具有公共终点的向量，不一定是共线向量，因此（1）不正确．
（2）两个向量不能比较大小，但它们的模能比较大小，正确．
（3）λ
=
（λ为实数），则λ=0或
=
，因此不正确．
（4）λ，μ为实数，若λ
=μ
，则
与
共线，正确．
综上可知：只有（2）（4）正确．
故选：B．
（2）两个向量不能比较大小，但它们的模能比较大小，正确．
（3）λ
| a |
| 0 |
| a |
| 0 |
（4）λ，μ为实数，若λ
| a |
| b |
| a |
| b |
综上可知：只有（2）（4）正确．
故选：B．
点评：本题综合考查了向量的定义、数乘、共线定理，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
已知实数x，y满足
，若z=ax+y的最大值为3a+9，最小值为3a-3，则实数a的取值范围为（ ）
|
| A、[-1，1] |
| B、[-1，2] |
| C、[2，3] |
| D、[-1，3] |
在下列四个选项中，说法错误的是（ ）
| A、若A是B的必要不充分条件，则非B也是非A的必要不充分条件 | |||||
B、“
| |||||
| C、“x≠1”是“x2≠1”的充分不必要条件 | |||||
| D、“x≠0”是“x+|x|＞0”的必要不充分条件 |
若x，y满足约束条件
，则目标函数z=2x+y的最大值是（ ）
|
| A、-3 | ||
B、
| ||
| C、2 | ||
| D、3 |
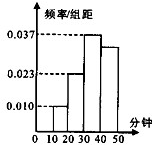学校为了了解学生每天课外阅读的时问（单位：分钟），抽取了n个学生进行调查，结果显示这些学生的课外阅读时间都在[10，50），其频率分布直方图如图所示，其中时间在[30，50）的学生有67人，则n的值是（ ）| A、100 | B、120 |
| C、130 | D、390 |
已知集合A={x|x2-3x＜0}，B={x||x-2|＜1}，则“a∈A”是“a∈B”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |