题目内容
4.已知椭圆C的左右焦点坐标分别是(-2,0),(2,0),离心率为$\frac{\sqrt{2}}{2}$,若P为椭圆C上的任意一点,过点P垂直于y轴的直线交y轴于点Q,M为线段QP的中点,则点M的轨迹方程为$\frac{{x}^{2}}{2}+\frac{{y}^{2}}{4}=1$.分析 利用焦点坐标qcc,离心率求出a,然后求解b,求出椭圆方程,然后设出M坐标,转化为P,代入求解即可.
解答 解:椭圆C的左右焦点坐标分别是(-2,0),(2,0),离心率为$\frac{\sqrt{2}}{2}$,
可得c=2,a=2$\sqrt{2}$,则b=2,
椭圆C的方程为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$,
设M(x,y)则P(2x,y)代入:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$,
可得:$\frac{{x}^{2}}{2}+\frac{{y}^{2}}{4}=1$.
则点M的轨迹方程为:$\frac{{x}^{2}}{2}+\frac{{y}^{2}}{4}=1$.
故答案为:$\frac{{x}^{2}}{2}+\frac{{y}^{2}}{4}=1$.
点评 本题考查轨迹方程的求法,转化思想的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.抛物线y2=4x上到焦点的距离等于3的点的坐标是( )
| A. | (2$\sqrt{2}$,2) | B. | (2$\sqrt{2}$,2)或(-2$\sqrt{2}$,2) | C. | (2,2$\sqrt{2}$) | D. | (2,2$\sqrt{2}$)或(2,-2$\sqrt{2}$) |
15. 某几何体的三视图如图所示,则其体积为( )
某几何体的三视图如图所示,则其体积为( )
 某几何体的三视图如图所示,则其体积为( )
某几何体的三视图如图所示,则其体积为( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
12.抛物线y=$\frac{1}{8}$x2的焦点坐标为( )
| A. | ($\frac{1}{32}$,0) | B. | (0,$\frac{1}{32}$) | C. | (0,4) | D. | (0,2) |
9.已知一组样本数据(xi,yi)如表
设其线性回归方程$\widehat{y}$=bx+a,若已求出b=0.7,则线性回归方程为( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | $\widehat{y}$=0.7x+0.35 | B. | $\widehat{y}$=0.7x+4.5 | C. | $\widehat{y}$=0.7x-0.35 | D. | $\widehat{y}$=0.7x-4.5 |
13.若实数x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y≥0\\ x≤0\end{array}\right.$,则z=x-2y的最小值是( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | -2 | D. | $-\frac{3}{2}$ |
14.等差数列{an}的前n项和为Sn,且a3+a9=16,则S11=( )
| A. | 88 | B. | 48 | C. | 96 | D. | 176 |
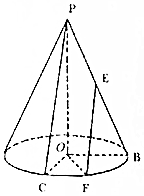 已知圆锥的高PO=4,底面半径OB=2,E为母线PB的中点,C为底面圆周上一点,满足OB⊥OC,F为弧BC上一点,且∠BOF=$\frac{π}{3}$.
已知圆锥的高PO=4,底面半径OB=2,E为母线PB的中点,C为底面圆周上一点,满足OB⊥OC,F为弧BC上一点,且∠BOF=$\frac{π}{3}$.