题目内容
16.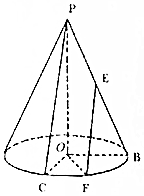 已知圆锥的高PO=4,底面半径OB=2,E为母线PB的中点,C为底面圆周上一点,满足OB⊥OC,F为弧BC上一点,且∠BOF=$\frac{π}{3}$.
已知圆锥的高PO=4,底面半径OB=2,E为母线PB的中点,C为底面圆周上一点,满足OB⊥OC,F为弧BC上一点,且∠BOF=$\frac{π}{3}$.(1)求证EF∥平面POC;
(2)求三棱锥E-OCF的体积.
分析 (1)如图所示,取OB的中点M,连接FM,FB,FB.利用等边三角形的性质可得FM⊥OB,又OB⊥OC,可得FM∥OC,可得FM∥平面POC.利用三角形中位线定理可得EM∥OP,可得EM∥平面POC.可得平面EFM∥平面POC.即可证明.
(2)由(1)可得EM⊥平面OBC,EM=$\frac{1}{2}OP$.S△OCF=$\frac{1}{2}×OC×OF×sin3{0}^{°}$.可得三棱锥E-OCF的体积V=$\frac{1}{3}×EM×{S}_{△OCF}$.
解答 解:(1)如图所示,取OB的中点M,连接FM,FB,FB.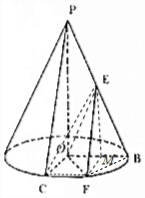 则△OFB为等边三角形,FM⊥OB,又OB⊥OC,
则△OFB为等边三角形,FM⊥OB,又OB⊥OC,
∴FM∥OC,又FM?平面POC,OC?平面POC.
∴FM∥平面POC.
又E为PB的中点,∴EM∥OP,同理可得EM∥平面POC.
又FM∩EM=M.
∴平面EFM∥平面POC.
∴EF∥平面POC.
(2)由(1)可得EM⊥平面OBC,EM=$\frac{1}{2}OP$=2.
S△OCF=$\frac{1}{2}×OC×OF×sin3{0}^{°}$=$\frac{1}{2}×{2}^{2}×\frac{1}{2}$=1.
∴三棱锥E-OCF的体积V=$\frac{1}{3}×EM×{S}_{△OCF}$=$\frac{1}{3}×2×1$=$\frac{2}{3}$.
点评 本题考查了线面面面平行与垂直的判定与性质定理、三棱锥的体积计算公式、,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.设D表示不等式组$\left\{\begin{array}{l}{x≤1}&{\;}\\{y≤x}&{\;}\\{x+y≥1}&{\;}\end{array}\right.$所确定的平面区域,在D内存在无数个点落在y=a(x+2)上,则a的取值范围是( )
| A. | R | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{1}{3}$) | D. | (-∞,0]∪[$\frac{1}{3}$,+∞) |
1.若直线l:(a2-1)x-y-2a+1=0不过第二象限,则a的取值范围为( )
| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,1] | D. | [1,+∞) |
8.已知sinα-sinβ=1-$\frac{\sqrt{3}}{2}$,cosα-cosβ=$\frac{1}{2}$,则cos(α-β)=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.已知复数z=$\frac{2i}{1-i}$,其中i 为虚数单位,则z所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.等差数列的前n项,前2n项,前3n项的和分别为A,B,C,则( )
| A. | A+C=2B | B. | B2=AC | C. | 3(B-A)=C | D. | A2+B2=A(B+C) |