题目内容

12．抛物线y=$\frac{1}{8}$x2的焦点坐标为（　　）
A．（$\frac{1}{32}$，0）B．（0，$\frac{1}{32}$）C．（0，4）D．（0，2）

分析 化简抛物线方程为标准方程，然后求解焦点坐标．

解答 解：抛物线y=$\frac{1}{8}$x2的标准方程为：x2=8y，所以抛物线y=$\frac{1}{8}$x2的焦点坐标为（0，2）．
故选：D．

点评 本题考查抛物线的简单性质的应用，是基础题．

练习册系列答案
相关题目
2．已知函数f（x）=ex+e-x，其中e是自然对数的底数．
（1）证明：f（x）是R上的偶函数；
（2）判断f（x）在（0，+∞）上的单调性，并证明．
3．某班共有50名学生，通过调查发现有30人同时在张老师和王老师的朋友圈，只有1人不在任何一个老师的朋友圈，且张老师的朋友圈比王老师的朋友圈多7人，则张老师的朋友圈有43人．
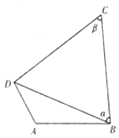20．如图，在圆内接四边形ABCD中，AB=2，AD=1，$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ
（Ⅰ）求角β的大小
（Ⅱ）求四边形ABCD周长的取值范围．
7．已知α∈（-$\frac{π}{2}$，0），cosα=$\frac{{\sqrt{5}}}{5}$．
（1）求sin2α的值；
（2）求$\frac{sinα+cosα}{sinα-cosα}$的值．
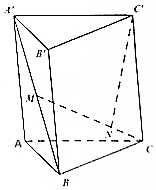17．如图，若在三棱柱ABC-A′B′C′中，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，$\overrightarrow{AA′}$=$\overrightarrow{c}$，M是A′B的中点，点N在CM上，且CN：NM=1：2，用$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$表示$\overrightarrow{CM}$、$\overrightarrow{C′N}$．
4．已知椭圆C的左右焦点坐标分别是（-2，0），（2，0），离心率为$\frac{\sqrt{2}}{2}$，若P为椭圆C上的任意一点，过点P垂直于y轴的直线交y轴于点Q，M为线段QP的中点，则点M的轨迹方程为$\frac{{x}^{2}}{2}+\frac{{y}^{2}}{4}=1$．
1．若直线l：（a2-1）x-y-2a+1=0不过第二象限，则a的取值范围为（　　）
A．（-∞，$\frac{1}{2}$]B．[$\frac{1}{2}$，+∞）C．（-∞，1]D．[1，+∞）
2．已知圆M的圆心在直线y=-x上，且经过点A（-3，0），B（1，2）．
（1）求圆M的方程；
（2）直线l与圆M相切，且l在y轴上的截距是在x轴上截距的两倍，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网