题目内容
已知定义在R上的奇函数f(x),设其导函数为f′(x),当x∈(-∞,0]时,恒有xf′(x)<f(-x),令F(x)=xf(x),则满足F(3)>F(2x-1)的实数x的取值范围是( )
A、(
| ||
| B、(-2,1) | ||
| C、(-1,2) | ||
D、(-1,
|
考点:利用导数研究函数的单调性
专题:函数的性质及应用,导数的综合应用
分析:根据已知条件利用函数的单调性和奇偶性构造出新函数,利用xf′(x)+f(x)<0,得到:[xf(x)]′<0,进一步分析出偶函数的单调性在对称区间内单调性相反.故建立不等式组,解不等式组求的结果.
解答:
解:定义在R上的奇函数f(x),
所以:f(-x)=-f(x)
设f(x)的导函数为f′(x),
当x∈(-∞,0]时,恒有xf′(x)<f(-x),
则:xf′(x)+f(x)<0
即:[xf(x)]′<0
所以:函数F(x)=xf(x)在(-∞,0)上是单调递减函数.
由于f(x)为奇函数,
令F(x)=xf(x),
则:F(x)为偶函数.
所以函数F(x)=xf(x)在(0,+∞)上是单调递增函数.
则:满足F(3)>F(2x-1)满足的条件是:
解得:
<x<2
所以x的范围是:(
,2)
故选:A
所以:f(-x)=-f(x)
设f(x)的导函数为f′(x),
当x∈(-∞,0]时,恒有xf′(x)<f(-x),
则:xf′(x)+f(x)<0
即:[xf(x)]′<0
所以:函数F(x)=xf(x)在(-∞,0)上是单调递减函数.
由于f(x)为奇函数,
令F(x)=xf(x),
则:F(x)为偶函数.
所以函数F(x)=xf(x)在(0,+∞)上是单调递增函数.
则:满足F(3)>F(2x-1)满足的条件是:
|
| 1 |
| 2 |
所以x的范围是:(
| 1 |
| 2 |
故选:A
点评:本题考查的知识要点:函数的性质的应用,单调性和奇偶性的应用,构造性函数解不等式组.属于基础题型.

练习册系列答案
相关题目
甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若S甲,S乙,S丙分别表示他们测试成绩的标准差,则( )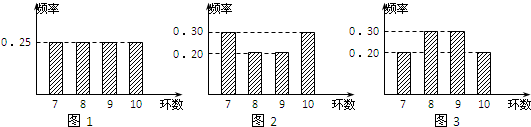

| A、S甲<S乙<S丙 |
| B、S甲<S丙<S乙, |
| C、S乙<S甲<S丙 |
| D、S丙<S甲<S乙 |
对任意x,y满足f(x+y2)=f(x)+2[f(y)]2,且f(1)≠0,则f(2013)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|