题目内容
甲，乙，丙三名运动员在某次测试中各射击20次，三人测试成绩的频率分布条形图分别如图1，图2和图3，若S甲，S乙，S丙分别表示他们测试成绩的标准差，则（ ）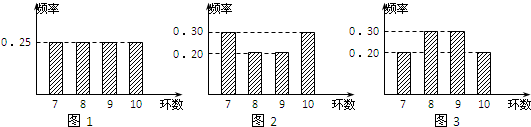
| A、S甲＜S乙＜S丙 |
| B、S甲＜S丙＜S乙， |
| C、S乙＜S甲＜S丙 |
| D、S丙＜S甲＜S乙 |
考点：极差、方差与标准差,众数、中位数、平均数
专题：概率与统计
分析：先分布求出甲，乙，丙三名运动员射击成绩的平均分，然后根据方差公式求出相应的方差，比较大小可得标准差的大小．
解答：
解：甲的平均成绩为（7+8+9+10）×0.25=8.5，
其方差为S甲2=0.25×[（7-8.5）2+（8-8.5）2+（9-8.5）2+（10-8.5）2]=1.25
乙的平均成绩为7×0.3+8×0.2+9×0.2+10×0.3=8.5，
其方差为S乙2=0.3×（7-8.5）2+0.2×（8-8.5）2+0.2×（9-8.5）2+0.3×（10-8.5）2=1.45
丙的平均成绩为7×0.2+8×0.3+9×0.3+10×0.2=8.5，
其方差为S丙2=0.2×（7-8.5）2+0.3×（8-8.5）2+0.3×（9-8.5）2+0.2×（10-8.5）2=1.05
∴S丙2＜S甲2＜S乙2
∴S丙＜S甲＜S乙．
故选：D．
其方差为S甲2=0.25×[（7-8.5）2+（8-8.5）2+（9-8.5）2+（10-8.5）2]=1.25
乙的平均成绩为7×0.3+8×0.2+9×0.2+10×0.3=8.5，
其方差为S乙2=0.3×（7-8.5）2+0.2×（8-8.5）2+0.2×（9-8.5）2+0.3×（10-8.5）2=1.45
丙的平均成绩为7×0.2+8×0.3+9×0.3+10×0.2=8.5，
其方差为S丙2=0.2×（7-8.5）2+0.3×（8-8.5）2+0.3×（9-8.5）2+0.2×（10-8.5）2=1.05
∴S丙2＜S甲2＜S乙2
∴S丙＜S甲＜S乙．
故选：D．
点评：本题主要考查了频率分布条形图，以及平均数、方差和标准差，同时考查了计算能力，属于基础题．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知定义在R上的奇函数f（x），设其导函数为f′（x），当x∈（-∞，0]时，恒有xf′（x）＜f（-x），令F（x）=xf（x），则满足F（3）＞F（2x-1）的实数x的取值范围是（ ）
A、（
| ||
| B、（-2，1） | ||
| C、（-1，2） | ||
D、（-1，
|
如图1，在Rt△ACB中，∠C=90°，BC=3，AC=6，D，E分别是AC，AB上的点，且DE∥BC，DE=2，将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图2．
已知平行六面体ABCD-A1B1C1D1，底面ABCD为菱形，∠BCD=∠C1CD=60°，求：当