题目内容
3．如图所示的程序框图所表示的算法功能是输出（ ）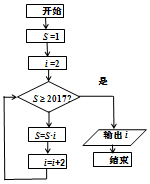
| A． | 使1×2×4×6×…×n≥2017成立的最小整数n | |
| B． | 使1×2×4×6×…×n≥2017成立的最大整数n | |
| C． | 使1×2×4×6×…×n≥2017成立的最小整数n+2 | |
| D． | 使1×2×4×6×…×n≥2017成立的最大整数n+2 |
分析 写出经过几次循环得到的结果，得到求的s的形式，判断出框图的功能．
解答 解：经过第一次循环得到s=1×3，i=5
经过第二次循环得到s=1×3×5，i=7
经过第三次循环得到s=1×3×5×7，i=8
…
s=1×3×5×7×…×i≥2017，i=i+2，
该程序框图表示算法的功能是求计算并输出使1×3×5×7×…×i≥2017成立的最小整数再加2，
故选：C
点评 本题考查程序框图，考查了循环体以及循环次数两个具体问题，常采用写出前几次循环的结果，找规律．属于基础题．
练习册系列答案
相关题目
已知函数$f（x）=2sin（2x+φ）\;（|φ|＜\frac{π}{2}）$部分图象如图所示．
14．有一个几何体的三视图及其尺寸如下（单位：cm），其侧视图和主视图是全等的三角形，则该几何体的表面积为（ ）
| A． | 12cm2 | B． | 15πcm2 | C． | 24πcm2 | D． | 36πcm2 |
8．若不等式$\frac{{a}^{2}+{b}^{2}}{2}$+1＞m（a+b）对任意正数a，b恒成立，则实数m的取值范围是（ ）
| A． | （-∞，$\frac{1}{2}$） | B． | （-∞，1） | C． | （-∞，2） | D． | （-∞，3） |
15．已知a∈R，命题“?x∈（0，+∞），等式lnx=a成立”的否定形式是（ ）
| A． | ?x∈（0，+∞），等式lnx=a不成立 | B． | ?x∈（-∞，0），等式lnx=a不成立 | ||
| C． | ?x0∈（0，+∞），等式lnx0=a不成立 | D． | ?x0∈（-∞，0），等式lnx0=a不成立 |
2．设x∈R，向量$\overrightarrow{a}$=（1，x），$\overrightarrow{b}$=（2，-4），且$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\overrightarrow{a}$•$\overrightarrow{b}$=（ ）
| A． | -6 | B． | $\sqrt{10}$ | C． | $\sqrt{5}$ | D． | 10 |
3．已知抛物线y2=2px（p＞0）上一点M到焦点F的距离等于3p，则直线MF的斜率为（ ）
| A． | ±$\sqrt{5}$ | B． | ±1 | C． | +$\frac{5}{2}$ | D． | ±$\frac{\sqrt{5}}{2}$ |