题目内容

14．有一个几何体的三视图及其尺寸如下（单位：cm），其侧视图和主视图是全等的三角形，则该几何体的表面积为（　　）
A．12cm2B．15πcm2C．24πcm2D．36πcm2

分析 先由几何体还原成原来的几何体，再根据三视图中的长度关系找到几何体中的长度关系即可求解

解答 解：由三视图知原几何体为一个圆锥，底面圆的半径为3，母线长为5
∴圆锥的表面积为S=$π×{3}^{2}+\frac{1}{2}×2π×3×5$=9π+15π=24π．
故选C

点评 本题考查三视图，由三视图求面积或体积，需根据三视图中的长度关系求出几何体中的长度关系，要求有比较好的空间想象力．属简单题．

练习册系列答案
相关题目
4．如图1，在梯形ABCD中，AB∥DC，∠ABC=90°，AB=2DC=2BC=4，O是边AB的中点，将三角形AOD饶边OD所在直线旋转到A，OD位置，使得∠A，OB=120°，如图2，设m为平面A1DC与平面A1OB的交线．

（1）判断直线DC与直线m的位置关系并证明；
（2）若在直线m上的点G满足OG⊥A1D，求出A1G的长；
（3）求直线A1O与平面A1BD所成角的正弦值．
5．已知Rt△ABC的周长为定值l，则它的面积最大值为$\frac{3-2\sqrt{2}}{4}$．
2．下列命题中的假命题是（　　）
A．?x∈R，3x＞0B．?x0∈R，lgx0=0
C．$?x∈（{0，\frac{π}{2}}），x＞sinx$D．$?{x_0}∈R，sin{x_0}+cos{x_0}=\sqrt{3}$
9．已知函数$f（x）=cos（2x-\frac{π}{3}）+2sin（x+\frac{π}{4}）sin（x-\frac{π}{4}）$．
（1）求f（x）的最小正周期；
（2）求f（x）在$[{-\frac{π}{4}，\frac{π}{4}}]$上的单调递增区间．
19．若某圆锥的母线长为2，侧面展开图为一个半圆，则该圆锥的表面积为3π．
6．已知函数f（x）=Asin（ωx+φ）+m（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）最小正周期为$\frac{π}{2}$，最大值为4，最小值为0，图象的一条对称轴为x=$\frac{π}{3}$
（1）求函数f（x）的解析式
（2）求函数f（x）的单调区间．
3．如图所示的程序框图所表示的算法功能是输出（　　）
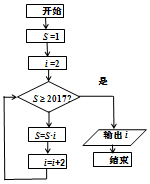
A．使1×2×4×6×…×n≥2017成立的最小整数n
B．使1×2×4×6×…×n≥2017成立的最大整数n
C．使1×2×4×6×…×n≥2017成立的最小整数n+2
D．使1×2×4×6×…×n≥2017成立的最大整数n+2
14．用数学归纳法证明：1+3+5+…+（2n-1）=n2（n∈N+）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网