题目内容
13. 已知函数$f(x)=2sin(2x+φ)\;(|φ|<\frac{π}{2})$部分图象如图所示.
已知函数$f(x)=2sin(2x+φ)\;(|φ|<\frac{π}{2})$部分图象如图所示.(Ⅰ)求f(x)的最小正周期及图中x0的值;
(Ⅱ)求f(x)在区间[0,$\frac{π}{2}$]上的最大值和最小值.
分析 (Ⅰ)根据函数的部分图象得出最小正周期T以及x0的值;
(Ⅱ)写出f(x)的解析式,利用正弦函数的图象与性质即可求出f(x)在区间[0,$\frac{π}{2}$]上的最值.
解答 解:(Ⅰ)∵函数$f(x)=2sin(2x+φ)\;(|φ|<\frac{π}{2})$,
∴函数的最小正周期为T=$\frac{2π}{2}$=π; …(2分)
因为点(0,1)在f(x)=2sin(2x+φ)的图象上,
所以2sin(2×0+φ)=1;
又因为|φ|<$\frac{π}{2}$,
所以φ=$\frac{π}{6}$,…(4分)
令2x+$\frac{π}{6}$=$\frac{π}{2}$,解得x=$\frac{π}{6}$,
所以x0=π+$\frac{π}{6}$=$\frac{7π}{6}$; …(6分)
(Ⅱ)由(Ⅰ)知f(x)=2sin(2x+$\frac{π}{6}$),
因为0≤x≤$\frac{π}{2}$,所以$\frac{π}{6}$≤2x+$\frac{π}{6}$≤$\frac{7π}{6}$;
当2x+$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{π}{6}$时,f(x)取得最大值2;
当2x+$\frac{π}{6}$=$\frac{7π}{6}$,即x=$\frac{π}{2}$时,f(x)取得最小值-1.…(13分)
点评 本题考查了根据正弦函数的部分图象求函数解析式的应用问题,是基础题目.

练习册系列答案
相关题目
18.如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
| A. | (1,+∞) | B. | (1,2) | C. | ($\frac{1}{2}$,1) | D. | (0,1) |
2.下列命题中的假命题是( )
| A. | ?x∈R,3x>0 | B. | ?x0∈R,lgx0=0 | ||
| C. | $?x∈({0,\frac{π}{2}}),x>sinx$ | D. | $?{x_0}∈R,sin{x_0}+cos{x_0}=\sqrt{3}$ |
3.如图所示的程序框图所表示的算法功能是输出( )
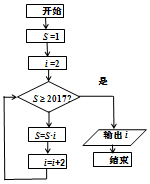

| A. | 使1×2×4×6×…×n≥2017成立的最小整数n | |
| B. | 使1×2×4×6×…×n≥2017成立的最大整数n | |
| C. | 使1×2×4×6×…×n≥2017成立的最小整数n+2 | |
| D. | 使1×2×4×6×…×n≥2017成立的最大整数n+2 |

 已知△ABD和△BCD是两个直角三角形,∠BAD=∠BDC=$\frac{π}{2}$,E、F分别是边AB、AD的中点,现将△ABD沿BD边折起到A1BD的位置,如图所示,使平面A1BD⊥平面BCD.
已知△ABD和△BCD是两个直角三角形,∠BAD=∠BDC=$\frac{π}{2}$,E、F分别是边AB、AD的中点,现将△ABD沿BD边折起到A1BD的位置,如图所示,使平面A1BD⊥平面BCD.