题目内容
11.已知$a=\int_0^π{sinxdx}$,则二项式${({1-\frac{a}{x}})^6}$的展开式中x-3的系数为-160.分析 求定积分得a的值,在二项展开式的通项公式中,令x的幂指数等于-3,求出r的值,即可求得展开式中x-3的系数.
解答 解:$a=\int_0^π{sinxdx}$=-cosx${|}_{0}^{π}$=2,
则二项式${({1-\frac{a}{x}})^6}$=${(1-\frac{2}{x})}^{6}$的展开式的通项公式为Tr+1=${C}_{6}^{r}$•(-2)r•x-r,
令-r=-3,可得r=3,故展开式中x-3的系数为${C}_{6}^{3}$•(-2)3=-160,
故答案为:-160.
点评 本题主要考查求定积分,二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
相关题目
2.下列命题中的假命题是( )
| A. | ?x∈R,3x>0 | B. | ?x0∈R,lgx0=0 | ||
| C. | $?x∈({0,\frac{π}{2}}),x>sinx$ | D. | $?{x_0}∈R,sin{x_0}+cos{x_0}=\sqrt{3}$ |
16.经过点A(3,2),且与直线x-y+3=0平行的直线方程是( )
| A. | x+y-1=0 | B. | x-y-1=0 | C. | x+y+1=0 | D. | x-y+1=0 |
3.如图所示的程序框图所表示的算法功能是输出( )
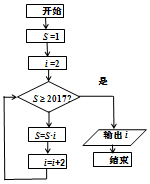

| A. | 使1×2×4×6×…×n≥2017成立的最小整数n | |
| B. | 使1×2×4×6×…×n≥2017成立的最大整数n | |
| C. | 使1×2×4×6×…×n≥2017成立的最小整数n+2 | |
| D. | 使1×2×4×6×…×n≥2017成立的最大整数n+2 |