题目内容
8.若不等式$\frac{{a}^{2}+{b}^{2}}{2}$+1>m(a+b)对任意正数a,b恒成立,则实数m的取值范围是( )| A. | (-∞,$\frac{1}{2}$) | B. | (-∞,1) | C. | (-∞,2) | D. | (-∞,3) |
分析 不等式$\frac{{a}^{2}+{b}^{2}}{2}$+1>m(a+b)对任意正数a,b恒成立,可得m<$\frac{{a}^{2}{+b}^{2}+2}{2(a+b)}$,再利用基本不等式的性质即可得出.
解答 解:∵不等式$\frac{{a}^{2}+{b}^{2}}{2}$+1>m(a+b)对任意正数a,b恒成立,
∴m<$\frac{{a}^{2}{+b}^{2}+2}{2(a+b)}$,
∵$\frac{{a}^{2}{+b}^{2}+2}{2(a+b)}$≥$\frac{\frac{{(a+b)}^{2}}{2}+2}{2(a+b)}$=$\frac{a+b}{4}$+$\frac{1}{a+b}$≥2$\sqrt{\frac{a+b}{4}•\frac{1}{a+b}}$=1.当且仅当a=b=1时取等号.
∴m<1,
故选:B.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
18.如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
| A. | (1,+∞) | B. | (1,2) | C. | ($\frac{1}{2}$,1) | D. | (0,1) |
16.经过点A(3,2),且与直线x-y+3=0平行的直线方程是( )
| A. | x+y-1=0 | B. | x-y-1=0 | C. | x+y+1=0 | D. | x-y+1=0 |
3.如图所示的程序框图所表示的算法功能是输出( )
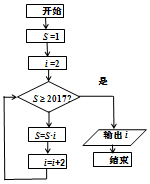

| A. | 使1×2×4×6×…×n≥2017成立的最小整数n | |
| B. | 使1×2×4×6×…×n≥2017成立的最大整数n | |
| C. | 使1×2×4×6×…×n≥2017成立的最小整数n+2 | |
| D. | 使1×2×4×6×…×n≥2017成立的最大整数n+2 |