题目内容

18．已知直线l过点（1，-1），且在y轴上的截距为$\frac{3}{2}$，则直线l的方程为5x+2y-3=0．

分析 由题意可得直线过点（0，$\frac{3}{2}$）和（1，-1），可得斜率，进而可得斜截式方程，化为一般式即可．

解答 解：∵直线在y轴上截距为$\frac{3}{2}$，
∴直线过点（0，$\frac{3}{2}$），
∴直线的斜率k=$\frac{\frac{3}{2}+1}{0-1}$=-$\frac{5}{2}$，
∴直线的方程为：y=-$\frac{5}{2}$x+$\frac{3}{2}$，
化为一般式可得：5x+2y-3=0，
故答案为：5x+2y-3=0．

点评 本题考查直线的方程，涉及直线的截距，属基础题．

练习册系列答案
相关题目
8．已知△ABD和△BCD是两个直角三角形，∠BAD=∠BDC=$\frac{π}{2}$，E、F分别是边AB、AD的中点，现将△ABD沿BD边折起到A1BD的位置，如图所示，使平面A1BD⊥平面BCD．
  （Ⅰ）求证：EF∥平面BCD；
（Ⅱ）求证：平面A1BC⊥平QUOTE A1BC⊥面A1CD；
（Ⅲ）请你判断，A1C与BD是否有可能垂直，做出判断并写明理由．
9．已知函数$f（x）=cos（2x-\frac{π}{3}）+2sin（x+\frac{π}{4}）sin（x-\frac{π}{4}）$．
（1）求f（x）的最小正周期；
（2）求f（x）在$[{-\frac{π}{4}，\frac{π}{4}}]$上的单调递增区间．
6．已知函数f（x）=Asin（ωx+φ）+m（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）最小正周期为$\frac{π}{2}$，最大值为4，最小值为0，图象的一条对称轴为x=$\frac{π}{3}$
（1）求函数f（x）的解析式
（2）求函数f（x）的单调区间．
13．已知f（x）=xlnx+mx，且曲线y=f（x）在点（1，f（1））处的切线斜率为1．
（1）求实数m的值；
（2）设$g（x）=f（x）-\frac{a}{2}{x^2}-x+a（{a∈R}）$在定义域内有两个不同的极值点x1，x2，求a的取值范围；
（3）已知λ＞0，在（2）的条件下，若不等式${e^{1+λ}}＜{x_1}•{x_2}^λ（{{x_1}＜{x_2}}）$恒成立，求λ的取值范围．
3．如图所示的程序框图所表示的算法功能是输出（　　）
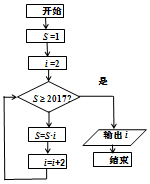
A．使1×2×4×6×…×n≥2017成立的最小整数n
B．使1×2×4×6×…×n≥2017成立的最大整数n
C．使1×2×4×6×…×n≥2017成立的最小整数n+2
D．使1×2×4×6×…×n≥2017成立的最大整数n+2
10．把数列{2n+1}依次按一项、二项、三项、四项循环分为（3），（5，7），（9，11，13），（15，17，19，21），（23），（25，27），（29，31，33），（35，37，39，41），…在第100个括号内的最后一个数字为501．
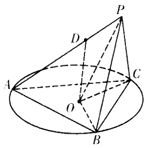7．如图所示，正三角形ABC的外接圆半径为2，圆心为O，PB=PC=2，D为AP上一点，AD=2DP，点D在平面ABC内的射影为圆心O．
（Ⅰ）求证：DO∥平面PBC；
（Ⅱ）求三棱锥O-PBC的体积．
18．已知函数f（x）=x2+2xsinθ-1，x∈[-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$]．
（1）当$θ=\frac{π}{6}$时，求函数f（x）的最小值；
（2）若函数f（x）在x∈[-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$]上是单调增函数，且θ∈[0，2π]，求θ的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网