题目内容
已知集合A={x|3≤3x≤27},B={x|log2x>1}.
(1)分别求A∩B,(∁RA)∪(∁RB);
(2)已知集合C={x|a<x<a2+1},若C⊆A,求满足条件的实数a的取值范围.
(1)分别求A∩B,(∁RA)∪(∁RB);
(2)已知集合C={x|a<x<a2+1},若C⊆A,求满足条件的实数a的取值范围.
考点:交、并、补集的混合运算,集合的包含关系判断及应用
专题:集合
分析:(1)先求出集合A,B,然后进行交、并、补的运算即可;
(2)因为C⊆A,所以分C=∅,和C≠∅两种情况,然后分别求a在这两种情况下的取值,再取并集即可.
(2)因为C⊆A,所以分C=∅,和C≠∅两种情况,然后分别求a在这两种情况下的取值,再取并集即可.
解答:
解:(1)A=[1,3],B=(2,+∞);
∴A∩B=(2,3],∁RA=(-∞,1)∪(3,+∞),∁RB=(-∞,2],(∁RA)∪(∁RB)=(-∞,2]∪(3,+∞);
(2)∵C⊆A,∴若C=∅,则a≥a2+1,解得a∈∅;
若C≠∅,则
,解得1≤a≤
;
∴实数a的取值范围为[1,
].
∴A∩B=(2,3],∁RA=(-∞,1)∪(3,+∞),∁RB=(-∞,2],(∁RA)∪(∁RB)=(-∞,2]∪(3,+∞);
(2)∵C⊆A,∴若C=∅,则a≥a2+1,解得a∈∅;
若C≠∅,则
|
| 2 |
∴实数a的取值范围为[1,
| 2 |
点评:考查指数函数,对数函数的单调性,以及根据单调性解不等式,集合的交、并、补的运算,子集的概念.

练习册系列答案
相关题目
点P是双曲线
-
=1上的一点,F1和F2分别是双曲线的左、右焦点,
•
=0,则△F1PF2的面积是( )
| x2 |
| 4 |
| y2 |
| 12 |
| PF1 |
| PF2 |
| A、24 | B、16 | C、8 | D、12 |
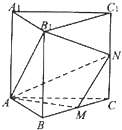 直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=
直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=