题目内容
点P是双曲线
-
=1上的一点,F1和F2分别是双曲线的左、右焦点,
•
=0,则△F1PF2的面积是( )
| x2 |
| 4 |
| y2 |
| 12 |
| PF1 |
| PF2 |
| A、24 | B、16 | C、8 | D、12 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设|
|=m,|
|=n,不妨设m>n.利用双曲线的定义可得m-n=4.由
•
=0,可得m2+n2=82,联立解得即可.
| PF1 |
| PF2 |
| PF1 |
| PF2 |
解答:
解:设|
|=m,|
|=n,不妨设m>n.
则m-n=4
∵
•
=0,∴m2+n2=82,
联立解得mn=24.
∴△F1PF2的面积=
mn=12.
故选:D.
| PF1 |
| PF2 |
则m-n=4
∵
| PF1 |
| PF2 |
联立解得mn=24.
∴△F1PF2的面积=
| 1 |
| 2 |
故选:D.
点评:本题考查了双曲线的定义标准方程及其性质、向量垂直与数量积的关系,属于基础题.

练习册系列答案
相关题目
在极坐标系中,圆C的圆心为(6,
),半径为5,直线θ=α(0≤α≤
,ρ∈R)被圆截得的弦长为8,则α的值为( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
“双曲线的方程为
-
=1”是“双曲线的渐近线方程为y=±
x”的( )
| x2 |
| 9 |
| y2 |
| 16 |
| 4 |
| 3 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4的值时,第一步算的是( )
| A、4×4=16 |
| B、7×4=28 |
| C、4×4×4=64 |
| D、7×4+6=34 |
已知曲线C1:ρ=2和曲线C2:ρcos(θ+
)=
,则C1上到C2的距离等于
的点的个数为( )
| π |
| 4 |
| 2 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
设A=
,B=
,则A与B的大小关系是( )
| x+1 |
| x+2 |
| x+3 |
| x+4 |
| A、A<B |
| B、A>B |
| C、仅有x>0,A<B |
| D、以上结论都不成立 |
已知△ABC中,AB=AC=5,BC=6,则△ABC的面积为( )
| A、12 | B、15 | C、20 | D、25 |
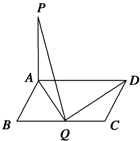 如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )
如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )