题目内容
已知奇函数f(x)在(-∞,0)∪(0,+∞)上有意义,且在(0,+∞)上是增函数,f(1)=0
(1)求满足不等式f(x)<0的实数x的取值范围;
(2)设函数g(θ)=sin2θ+m•cosθ-2m,若集合M={m|g(θ)<0},集合 N={m|f[g(θ)]<0},求M∩N.
(1)求满足不等式f(x)<0的实数x的取值范围;
(2)设函数g(θ)=sin2θ+m•cosθ-2m,若集合M={m|g(θ)<0},集合 N={m|f[g(θ)]<0},求M∩N.
考点:函数奇偶性的性质,交集及其运算,函数单调性的性质
专题:综合法,函数的性质及应用
分析:根据奇偶性,判断出f (x) 在 (-∞,0)上也是增函数,列出不等式,求解即可.
(2)利用换元的思想转化不等式,再求解集合解集,得出所求集合的解集,最后分类求解集合的综合问题.
(2)利用换元的思想转化不等式,再求解集合解集,得出所求集合的解集,最后分类求解集合的综合问题.
解答:
解:依题意,f (-1)=-f (1)=0,又f (x) 在 (0,+∞) 上是增函数,
∴f (x) 在 (-∞,0)上也是增函数,
∴由 f (x)<0得x<-1或0<x<1
∴N={m|f[g(θ)]<0}={m|g(θ)<-1或0<g(θ)<1},
M∩N={m|g(θ)<-1}
由g(θ)<-1得 sin2θ+m cos θ-2m<-1⇒cos2θ-m cos θ+2m-2>0 恒成立
⇒(cos2θ-m cos θ+2m-2)min>0
设t=cosθ,h(t)=cos2θ-m cos θ+2m-2=t2-mt+2m-2
=(t-
)2-
+2m-2,∵cosθ∈[-1,1]⇒t∈[-1,1],h(t) 的对称轴为 t=
1° 当
>1,即 m>2 时,h(t) 在[-1,1]为减函数
∴h(t)min=h(1)=m-1>0⇒m>1⇒m>2)
2° 当-1≤
≤1,即-2≤m≤2 时,
∴h(t)min=h(
)=-
+2m-2>0⇒4-2
<m<4+2
⇒4-2
<m≤2
3° 当
<-1,即 m<-2 时,h(t) 在[-1,1]为增函数
∴h(t)min=h(-1)=3m-1>0⇒m>
无解
综上,m>4-2
⇒M∩N={m|m>4-2
另解:依题意,f (-1)=-f (1)=0,又f (x) 在 (0,+∞) 上是增函数,
∴f (x) 在 (-∞,0)上也是增函数,
∴由 f (x)<0得x<-1或0<x<1,
∴N={m|f[g(θ)]<0}={m|g(θ)<-1或0<g(θ)<1},
由g(θ)<-1得 sin2θ+m cos θ-2m<-1⇒cos2θ-m cos θ+2m-2>0 恒成立
⇒(cos2θ-m cos θ+2m-2)min>0M∩N={m|g(θ)<-1}由g(θ)<-1得 sin2θ+m cos θ-2m<-1⇒cos2θ-m cos θ+2m-2>0 恒成立
⇒(cos2θ-m cos θ+2m-2)min>0
设t=cosθ,h(t)=cos2θ-m cos θ+2m-2=t2-mt+2m-2
=(t-
)2-
+2m-2,∵cosθ∈[-1,1]⇒t∈[-1,1],h(t) 的对称轴为 t=
∵cosθ∈[]
综上所得,m>4-2
⇒M∩N={m|m>4-2
}
∴f (x) 在 (-∞,0)上也是增函数,
∴由 f (x)<0得x<-1或0<x<1
∴N={m|f[g(θ)]<0}={m|g(θ)<-1或0<g(θ)<1},
M∩N={m|g(θ)<-1}
由g(θ)<-1得 sin2θ+m cos θ-2m<-1⇒cos2θ-m cos θ+2m-2>0 恒成立
⇒(cos2θ-m cos θ+2m-2)min>0
设t=cosθ,h(t)=cos2θ-m cos θ+2m-2=t2-mt+2m-2
=(t-
| m |
| 2 |
| m2 |
| 4 |
| m |
| 2 |
1° 当
| m |
| 2 |
∴h(t)min=h(1)=m-1>0⇒m>1⇒m>2)
2° 当-1≤
| m |
| 2 |
∴h(t)min=h(
| m |
| 2 |
| m2 |
| 4 |
| 2 |
| 2 |
| 2 |
3° 当
| m |
| 2 |
∴h(t)min=h(-1)=3m-1>0⇒m>
| 1 |
| 3 |
综上,m>4-2
| 2 |
| 2 |
另解:依题意,f (-1)=-f (1)=0,又f (x) 在 (0,+∞) 上是增函数,
∴f (x) 在 (-∞,0)上也是增函数,
∴由 f (x)<0得x<-1或0<x<1,
∴N={m|f[g(θ)]<0}={m|g(θ)<-1或0<g(θ)<1},
由g(θ)<-1得 sin2θ+m cos θ-2m<-1⇒cos2θ-m cos θ+2m-2>0 恒成立
⇒(cos2θ-m cos θ+2m-2)min>0M∩N={m|g(θ)<-1}由g(θ)<-1得 sin2θ+m cos θ-2m<-1⇒cos2θ-m cos θ+2m-2>0 恒成立
⇒(cos2θ-m cos θ+2m-2)min>0
设t=cosθ,h(t)=cos2θ-m cos θ+2m-2=t2-mt+2m-2
=(t-
| m |
| 2 |
| m2 |
| 4 |
| m |
| 2 |
∵cosθ∈[]
综上所得,m>4-2
| 2 |
| 2 |
点评:考查了函数的奇偶性,单调性,结合不等式解决问题,综合考察解决问题的能力.

练习册系列答案
相关题目
“双曲线的方程为
-
=1”是“双曲线的渐近线方程为y=±
x”的( )
| x2 |
| 9 |
| y2 |
| 16 |
| 4 |
| 3 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知△ABC中,AB=AC=5,BC=6,则△ABC的面积为( )
| A、12 | B、15 | C、20 | D、25 |
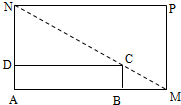 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米.