题目内容
从4名女同学和6名男同学中,选出3名女同学和4名男同学,7人排成一排.
(1)如果选出的7人中,3名女同学必须站在一起,共有多少种排法?
(2)如果选出的7人中,3名女同学互不相邻,共有多少种排法?
(注:必须用数字表示最终结果)
(1)如果选出的7人中,3名女同学必须站在一起,共有多少种排法?
(2)如果选出的7人中,3名女同学互不相邻,共有多少种排法?
(注:必须用数字表示最终结果)
考点:计数原理的应用
专题:排列组合
分析:(1)根据先选后排排的原则,先4名女同学和6名男同学中,选出3名女同学和4名男同学,再根据相邻问题用捆绑法,根据分步计数原理可得.
(2)根据先选后排排的原则,先4名女同学和6名男同学中,选出3名女同学和4名男同学,再根据不相邻问题用插空法,根据分步计数原理可得.
(2)根据先选后排排的原则,先4名女同学和6名男同学中,选出3名女同学和4名男同学,再根据不相邻问题用插空法,根据分步计数原理可得.
解答:
解:(1)先选人,有
种选法,再把3名女同学看成一个元素,与其余4名男同学相当于5个元素进行全排列,然后3名女同学再进行全排列,由分步计数原理,共有
=43200种排法
(2)选完人后,先让4名男同学全排列,再把3名女同学在每两男生之间(含两端)的5个位置中插入排列,共有
=86400种排法.
| C | 3 4 |
| C | 4 6 |
| C | 3 4 |
| C | 4 6 |
| A | 5 5 |
| A | 3 3 |
(2)选完人后,先让4名男同学全排列,再把3名女同学在每两男生之间(含两端)的5个位置中插入排列,共有
| C | 3 4 |
| C | 4 6 |
| A | 4 4 |
| A | 3 5 |
点评:本题主要考查了排列组合的问题,相邻用捆绑,不相邻用插空,属于基础题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
在极坐标系中,圆C的圆心为(6,
),半径为5,直线θ=α(0≤α≤
,ρ∈R)被圆截得的弦长为8,则α的值为( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
设A=
,B=
,则A与B的大小关系是( )
| x+1 |
| x+2 |
| x+3 |
| x+4 |
| A、A<B |
| B、A>B |
| C、仅有x>0,A<B |
| D、以上结论都不成立 |
已知△ABC中,AB=AC=5,BC=6,则△ABC的面积为( )
| A、12 | B、15 | C、20 | D、25 |
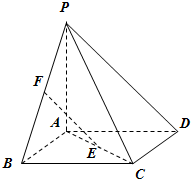 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证:
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证: