题目内容
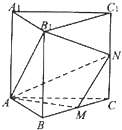 直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=
直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=| 2 |
(1)二面角B1-AN-M的大小;
(2)C1到平面AMN的距离.
考点:点、线、面间的距离计算,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:法一:(1)建立坐标系,利用向量法能求出二面角B1-AN-M的大小.
(2)求出
=(0,0,1),利用向量法能求出C1到平面AMN的距离.
法二:(1)由已知AM⊥BC,BC=2,AM=1,AM⊥平面BCC1B1,平面⊥AMN⊥平面BCC1B1,作B1H⊥MN于H,HR⊥AN于R,连B1R,∠B1RH是二面角B1-AN-M的平面角,由此能求出二面角B1-AN-M的大小.
(2)由已知得C1到平面AMN的距离等于C到平面AMN的距离,设C到平面AMN的距离为h,由VC-AMN=VN-AMC,能求出结果.
(2)求出
| NC1 |
法二:(1)由已知AM⊥BC,BC=2,AM=1,AM⊥平面BCC1B1,平面⊥AMN⊥平面BCC1B1,作B1H⊥MN于H,HR⊥AN于R,连B1R,∠B1RH是二面角B1-AN-M的平面角,由此能求出二面角B1-AN-M的大小.
(2)由已知得C1到平面AMN的距离等于C到平面AMN的距离,设C到平面AMN的距离为h,由VC-AMN=VN-AMC,能求出结果.
解答:
解法一:
解:(1)建立坐标系如图所示,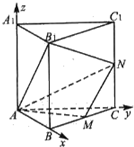
则A(0,0,0),M(
,
,0),N(0,
,1),B1(
0,2),…1分
=(
,
,0),
=(0,
,1),
=(
,0,2)
设平面AMN的法向量为
=(p,q,r),
平面AB1N的法向量为
=(s,t,k)…2分
由
•
=0,
•
=0,得
p+
q=0,
q+r=0,
令p=1,则q=-1,r=
,于是
=(1,-1,
).…3分
由
•
=0,
•
=0,得
s+2k=0,
t+k=0,
令k=-
,则s=2,t=1,于是
=(2,1,-
).…4分
•
=-1,|
|=
=2,|
|=
=
,
cos<
,
>
=-
…5分
∵二面角B1-AN-M的大小arccos
.…6分
(2)∵
=(0,0,1),
∴C1到平面AMN的距离:d=
=
.…12分
解法二:
解:(1)∵∠BAC=90°,AB=AC=
,M是棱BC的中点.
∴AM⊥BC,BC=2,AM=1,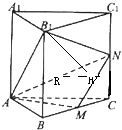
∴AM⊥平面BCC1B1,
∴平面⊥AMN⊥平面BCC1B1.…2分
作B1H⊥MN于H,HR⊥AN于R,连B1R
∵平面AMN∩平面BCC1B1=MN
∴B1H⊥平面⊥AMN,又由三垂线定理知,B1R⊥AN,
∴∠B1RH是二面角B1-AN-M的平面角…3分
由已知得 AN=
,MN=
B1M=
=B1N,
则B1H=
,
又Rt△AMN~Rt△HRN,
=
,
∴RH=
,
∴B1R=
=
cos∠B1RH=
=
…5分
∴二面角B1-AN-M的大小arcos
.…6分
(2)∵N是CC1中点
∴C1到平面AMN的距离等于C到平面AMN的距离
设C到平面AMN的距离为h,
由VC-AMN=VN-AMC,
得
×
AM•MN•h=
×
AM•MC,
∴h=
.…12分
解:(1)建立坐标系如图所示,

则A(0,0,0),M(
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2, |
| AM |
| ||
| 2 |
| ||
| 2 |
| AN |
| 2 |
| AB |
| 2 |
设平面AMN的法向量为
| m |
平面AB1N的法向量为
| n |
由
| AM |
| m |
| AN |
| m |
| ||
| 2 |
| ||
| 2 |
| 2 |
令p=1,则q=-1,r=
| 2 |
| m |
| 2 |
由
| AB1 |
| n |
| AN |
| n |
| 2 |
| 2 |
令k=-
| 2 |
| n |
| 2 |
| m |
| n |
| m |
| 1+1+2 |
| n |
| 4+1+2 |
| 7 |
cos<
| m |
| n |
| -1 | ||
2×
|
| ||
| 14 |
∵二面角B1-AN-M的大小arccos
| ||
| 14 |
(2)∵
| NC1 |
∴C1到平面AMN的距离:d=
|
| ||||
|
|
| ||
| 2 |
解法二:
解:(1)∵∠BAC=90°,AB=AC=
| 2 |
∴AM⊥BC,BC=2,AM=1,

∴AM⊥平面BCC1B1,
∴平面⊥AMN⊥平面BCC1B1.…2分
作B1H⊥MN于H,HR⊥AN于R,连B1R
∵平面AMN∩平面BCC1B1=MN
∴B1H⊥平面⊥AMN,又由三垂线定理知,B1R⊥AN,
∴∠B1RH是二面角B1-AN-M的平面角…3分
由已知得 AN=
| 3 |
| 2 |
| 5 |
则B1H=
3
| ||
| 2 |
又Rt△AMN~Rt△HRN,
| RH |
| AM |
| HN |
| AN |
∴RH=
| ||
| 6 |
∴B1R=
| HR2+B1H2 |
|
| RH |
| B1R |
| ||
| 14 |
∴二面角B1-AN-M的大小arcos
| ||
| 14 |
(2)∵N是CC1中点
∴C1到平面AMN的距离等于C到平面AMN的距离
设C到平面AMN的距离为h,
由VC-AMN=VN-AMC,
得
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴h=
| ||
| 2 |
点评:本题考查二面角的大小的求法,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4的值时,第一步算的是( )
| A、4×4=16 |
| B、7×4=28 |
| C、4×4×4=64 |
| D、7×4+6=34 |
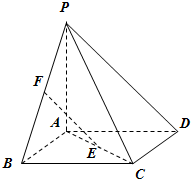 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证:
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证: (理)如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面ABCD,在BC边上取点E,使得PE⊥DE,则满足条件的E点有两个时,求实数a的取值范围.
(理)如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面ABCD,在BC边上取点E,使得PE⊥DE,则满足条件的E点有两个时,求实数a的取值范围.