题目内容
6.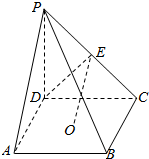 如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.(Ⅰ)证明:EO∥平面PAD;
(Ⅱ)证明:DE⊥平面PBC.
分析 (Ⅰ)连接AC,则PA∥EO,由此能证明EO∥平面PAD.
(Ⅱ)推导出BC⊥DC,BC⊥DE,从而DE⊥PC,由此能证明DE⊥平面PBC.
解答  (本小题满分12分)
(本小题满分12分)
证明:(Ⅰ)连接AC,∵点O是底面正方形ABCD的中心,
∴点O是AC的中点,又∵E是PC的中点,
在△PAC中,EO是中位线,∴PA∥EO…(4分)
∵EO?平面PAD,PA?平面PAD
∴EO∥平面PAD…(5分)
(Ⅱ)∵PD⊥平面ABCD,且PD?平面PCD,
∴平面PDC⊥平面ABCD,∵底面ABCD是正方形,有BC⊥DC,
又平面ABCD∩平面PCD=CD,∴BC⊥平面PDC.
而DE?平面PDC,∴BC⊥DE. ①…(9分)
∵PD=DC,可知△PDC是等腰直角三角形,
而DE是斜边PC的中线,
∴DE⊥PC. ②…(11分)
又BC,PC?平面PBC,且BC∩PC=C,
∴DE⊥平面PBC.…(12分)
点评 本题考查线面平行的证明,考查线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17.“m≥0”是“直线mx-y+1-m=0与圆(x-1)2+y2=1相切”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.给定空间直角坐标系中,x轴上到点P(4,1,2)的距离为$\sqrt{30}$的点有( )
| A. | 2个 | B. | 1个 | C. | 0个 | D. | 无数个 |
15.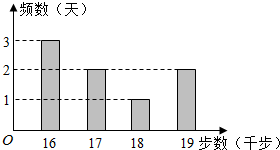 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).
(Ⅰ)求小王这8天“健步走”步数的平均数;
(Ⅱ)从步数为16千步,17千步,18千步的几天中任选2天,设小王这2天通过健步走消耗的“能量和”为X,求X的分布列.
 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).| 健步走步数(千卡) | 16 | 17 | 18 | 19 |
| 消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(Ⅱ)从步数为16千步,17千步,18千步的几天中任选2天,设小王这2天通过健步走消耗的“能量和”为X,求X的分布列.
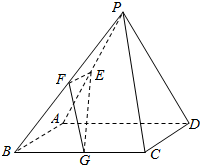 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,且平面PAD⊥平面ABCD,E,F,G分别是PA、PB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,且平面PAD⊥平面ABCD,E,F,G分别是PA、PB、BC的中点.