题目内容
14.已知圆C1:x2-2x+y2=0,圆C2:(x+3)2+(y-4)2=1,若过点C1的直线l被圆C2所截得的弦长为$\frac{6}{5}$,则直线l的方程为4x+3y-4=0或3x+4y-3=0.分析 过点C1的直线l被圆C2所截得的弦长为$\frac{6}{5}$,可得圆心到直线的距离d=$\sqrt{1-\frac{9}{25}}$=$\frac{4}{5}$,故可设出直线的点斜式方程,利用圆心(-3,4)到直线的距离d=$\frac{|-3k-4+k|}{\sqrt{{k}^{2}+1}}$=$\frac{4}{5}$,求出k值,进而得到直线方程.
解答 解:圆圆C1:x2-2x+y2=0,化为标准方程为(x-1)2+y2=1.
∵过点C1的直线l被圆C2所截得的弦长为$\frac{6}{5}$,
∴圆心到直线的距离d=$\sqrt{1-\frac{9}{25}}$=$\frac{4}{5}$
由题意,所求直线的斜率存在,设为k,则直线方程为y=k(x+1),即kx-y+k=0
∴圆心(-3,4)到直线的距离d=$\frac{|-3k-4+k|}{\sqrt{{k}^{2}+1}}$=$\frac{4}{5}$
∴k=-$\frac{4}{3}$或-$\frac{3}{4}$
∴此时直线方程为4x+3y-4=0或3x+4y-3=0.
故答案为:4x+3y-4=0或3x+4y-3=0.
点评 本题考查的知识点是直线和圆的方程的应用,直线的一般式方程,考查计算能力,属于中档题.

练习册系列答案
相关题目
4.下列函数中,是偶函数的是( )
| A. | y=2x | B. | y=x2 | C. | y=2x | D. | y=log2x |
4.在平行四边形ABCD中,对角线AC与BD交于点O,$\overrightarrow{CO}=λ({\overrightarrow{AB}+\overrightarrow{AD}})$,则实数λ=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
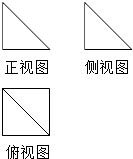 一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.
一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.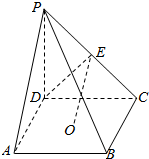 如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.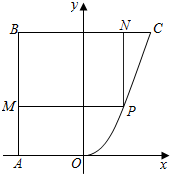 某地有如图所示的一块不规则的非农业用地ABCO,且AB⊥BC,OA∥BC,AB=BC=4km,AO=2km,曲线段OC是以O为顶点,开口向上,且对称轴平行于AB的抛物线的一段.当地政府为科技兴市,欲将该地规划建成一个矩形高科技工业园区PMBN,矩形的相邻两边BM,BN分别落在AB,BC上,顶点P在曲线段OC上.问应如何规划才能使矩形园区的用地面积最大?并求出最大的用地面积(精确到0.1 km2).
某地有如图所示的一块不规则的非农业用地ABCO,且AB⊥BC,OA∥BC,AB=BC=4km,AO=2km,曲线段OC是以O为顶点,开口向上,且对称轴平行于AB的抛物线的一段.当地政府为科技兴市,欲将该地规划建成一个矩形高科技工业园区PMBN,矩形的相邻两边BM,BN分别落在AB,BC上,顶点P在曲线段OC上.问应如何规划才能使矩形园区的用地面积最大?并求出最大的用地面积(精确到0.1 km2).