题目内容
17.“m≥0”是“直线mx-y+1-m=0与圆(x-1)2+y2=1相切”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 直线mx-y+1-m=0过点(1,1),利用直线mx-y+1-m=0与圆(x-1)2+y2=1相切,可得m=0,即可得出结论.
解答 解:直线mx-y+1-m=0过点(1,1)
∵直线mx-y+1-m=0与圆(x-1)2+y2=1相切,
∴m=0,
∴“m≥0”是“直线mx-y+1-m=0与圆(x-1)2+y2=1相切”的必要不充分条件,
故选:B.
点评 本题考查直线与圆的位置关系,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
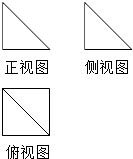 一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.
一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.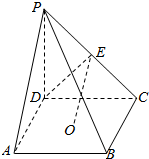 如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.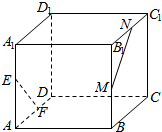 已知点E,F,M,N分别为正方体ABCD-A1B1C1D1的棱AA1,AD,BB1,B1C1的中点,则异面直线EF和MN所成的角为90°.
已知点E,F,M,N分别为正方体ABCD-A1B1C1D1的棱AA1,AD,BB1,B1C1的中点,则异面直线EF和MN所成的角为90°.