题目内容
16.在△ABC中,角A,B,C的对边分别为a,b,c,且满足ccosB=(2a+b)cos(π-C).(1)求角C的大小;
(2)若c=4,△ABC的面积为$\sqrt{3}$,求a+b的值.
分析 (1)由诱导公式,正弦定理化简已知可得sinCcosB=(-2sinA-sinB)cosC,利用三角函数恒等变换的应用化简可得
cosC=-$\frac{1}{2}$,即可得解C的值.
(2)利用三角形面积公式可求得ab=4,利用余弦定理即可求得a+b的值.
解答 解:(1)∵ccosB=(2a+b)cos(π-C).
∴sinCcosB=(-2sinA-sinB)cosC,
∴sin(B+C)=-2sinAcosC,
∴cosC=-$\frac{1}{2}$,
∴C=$\frac{2π}{3}$.
(2)由${S}_{△ABC}=\frac{1}{2}absinC=\sqrt{3}$,可得:ab=4,
由余弦定理可得:c2=a2+b2+ab=(a+b)2-ab=16,
解得:a+b=2$\sqrt{5}$.
点评 本题主要考查了诱导公式,正弦定理,余弦定理,三角形面积公式,三角函数恒等变换的应用,属于中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
4.在平行四边形ABCD中,对角线AC与BD交于点O,$\overrightarrow{CO}=λ({\overrightarrow{AB}+\overrightarrow{AD}})$,则实数λ=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
11.已知P是直线;“3x+4y+13=0的动点,PA是圆C:x2+y2-2x-2y-2=0的一条切线,A是切点,那么△PAC的面积的最小值是( )
| A. | 5$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
1.有分别写着数字1到120的120张卡片,从中取出1张,这样卡片上的数字是2的倍数或是3的倍数的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{2}{3}$ |
8.下列命题正确的是( )
| A. | 若a2>b2,则a>b | B. | 若|a|>b,则a2>b2 | C. | 若a>|b|,则a2>b2 | D. | 若a>b,则a2>b2 |
6.如图,Rt△A′O′B′的直观图,且△A′O′B′为面积为1,则△AOB中最长的边长为( )


| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 1 | D. | 2 |
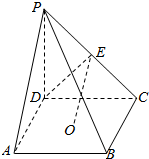 如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.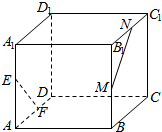 已知点E,F,M,N分别为正方体ABCD-A1B1C1D1的棱AA1,AD,BB1,B1C1的中点,则异面直线EF和MN所成的角为90°.
已知点E,F,M,N分别为正方体ABCD-A1B1C1D1的棱AA1,AD,BB1,B1C1的中点,则异面直线EF和MN所成的角为90°.