题目内容
1.给定空间直角坐标系中,x轴上到点P(4,1,2)的距离为$\sqrt{30}$的点有( )| A. | 2个 | B. | 1个 | C. | 0个 | D. | 无数个 |
分析 设点A的坐标是(x,0,0),由题意|PA|=$\sqrt{(x-4)^{2}+{1}^{2}+{2}^{2}}$=$\sqrt{30}$,由此能求出结果.
解答 解:设点A的坐标是(x,0,0),
由题意|PA|=$\sqrt{(x-4)^{2}+{1}^{2}+{2}^{2}}$=$\sqrt{30}$,
∴(x-4)2=25.解得x=9或x=-1.
∴点A坐标为(9,0,0)或(-1,0,0).
∴给定空间直角坐标系中,x轴上到点P(4,1,2)的距离为$\sqrt{30}$的点有2个.
故选:A.
点评 本题考查满足条件的点的个数的求法,是中档题,解题时要认真审题,注意空间中两点间距离公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知P是直线;“3x+4y+13=0的动点,PA是圆C:x2+y2-2x-2y-2=0的一条切线,A是切点,那么△PAC的面积的最小值是( )
| A. | 5$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
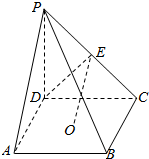 如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.