Question

已知f（x）=x²-2x，x∈[t，t+2]，
（1）求f（x）的最大值M（t）；
（2）求f（x）的最小值m（t）；
（3）求g（t）=M（t）-m（t）的表达式，并作出图象，指出g（t）的最小值．

Answer 1

考点：二次函数在闭区间上的最值

专题：函数的性质及应用

分析：（1）求二次函数f（x）的对称轴x=1，讨论区间[t，2t]和对称轴的关系，根据函数f（x）的单调性或比较端点值便可求出f（x）的最大值M（t）；
（2）根据（1）求最大值的过程即可求出最小值m（t）；
（3）将求得的M（t），m（t）带入g（t），即可求出g（t），作出g（t）的函数图象，根据图象求g（t）的最小值即可．

解答： 解：（1）f（x）=x²-2x=（x-1）²-1；
①若t+2≤1，即t≤-1，f（x）在[t，t+2]上单调递减，∴M（t）=f（t）=t²-2t；
②若t＜1＜t+2，即-1＜t＜1：若-1＜t≤0，则f（t）＞f（t+2），∴M（t）=f（t）=t²-2t；若0＜t＜1，则f（t+2）＞f（t），∴M（t）=f（t+2）=t²+2t；
③若t≥1，f（x）在[t，t+2]上单调递增，∴M（t）=f（t+2）=t²+2t；
∴M(t)=

t2-2t t≤0 t2+2t t＞0

；
（2）由（1）知，t≤-1时，m（t）=f（t+2）=t²+2t；
-1＜t＜1时，m（t）=f（1）=-1；
t≥1时，m（t）=f（t）=t²-2t；
∴m(t)=

t2+2t t≤-1 -1 -1＜t＜1 t2-2t t≥1

；
（3）由（1）（2）得：
g(t)=

-4t t≤-1 t2-2t+1 -1＜t≤0 t2+2t+1 0＜t＜1 4t t≥1

，图象如下：
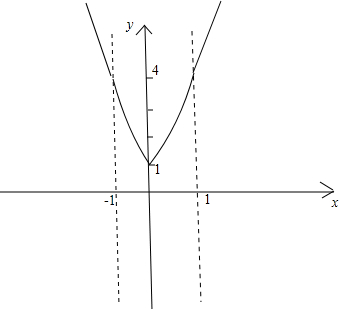由图象可看出g（t）的最小值为1．

点评：考查根据二次函数的单调性以及端点值，顶点求f（x）最值的方法，以及通过图象求最小值的方法．