题目内容
已知函数f(x)=
x3+2x2+ax+b,g(x)=ex(cx+d),且函数f(x)的导函数为f′(x),若曲线f(x)和g(x)都过点A(0,2),且在点A 处有相同的切线y=4x+2.
(Ⅰ)求a,b,c,d的值;
(Ⅱ)若x≥-2时,mg(x)≥f′(x)-2恒成立,求实数m的取值范围.
| 1 |
| 3 |
(Ⅰ)求a,b,c,d的值;
(Ⅱ)若x≥-2时,mg(x)≥f′(x)-2恒成立,求实数m的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的概念及应用
分析:(I)对f(x),g(x)进行求导,已知在交点处有相同的切线及曲线y=f(x)和曲线y=g(x)都过点P(0,2),从而解出a,b,c,d的值;
(II)令φ(x)=2mex(x+1)-x2-4x-2,求出导函数,令φ'(x)=0得x1=-lnm,x2=-2,通过对m的讨论,确定函数的单调性,可得最值,即可求出m的范围.
(II)令φ(x)=2mex(x+1)-x2-4x-2,求出导函数,令φ'(x)=0得x1=-lnm,x2=-2,通过对m的讨论,确定函数的单调性,可得最值,即可求出m的范围.
解答:
解:(I)由已知得f(0)=2,g(0)=2,f'(0)=4,g'(0)=4,
而f'(x)=x2+4x+a,g'(x)=ex(cx+d+c)
故b=2,d=2,a=4,c=2…(4分)
(Ⅱ)令φ(x)=2mex(x+1)-x2-4x-2,
则φ'(x)=2mex(x+2)-2x-4=2(x+2)(mex-1)
因φ(0)≥0,则m≥1
令φ'(x)=0得x1=-lnm,x2=-2…(6分)
(1)若1≤m<e2,则-2<x1≤0,从而x∈(-2,x1)时φ'(x)<0;当x∈(x1,+∞)时φ'(x)>0,即φ(x)在 (-2,x1)单调递减,在(x1,+∞)单调递增,故φ(x)在[-2,+∞)的最小值φ(x1),φ(x1)=2mex1(x1+1)-
-4x1-4=2x1+2-
-4x1-2=-
-2x1=-x1(x1+2)≥0
故当x≥-2时φ(x)≥0,即mg(x)≥f'(x)+2恒成立. …(8分)
(2)若m=e2,则φ'(x)=2e2(x+2)(ex-e-2),从而当x≥-2时φ'(x)≥0,即φ(x)在[-2,+∞)单调递增,而φ(-2)=0,故当x≥-2时φ(x)≥0,即mg(x)≥f'(x)+2恒成立.
(3)若m>e2,则φ(-2)=-2me-2+2=-2e-2(m-e2)<0,从而当x≥-2时,mg(x)≥f'(x)+2不可能恒成立. …(11分)
综上:m的取值范围是[1,e2]…(12分)
而f'(x)=x2+4x+a,g'(x)=ex(cx+d+c)
故b=2,d=2,a=4,c=2…(4分)
(Ⅱ)令φ(x)=2mex(x+1)-x2-4x-2,
则φ'(x)=2mex(x+2)-2x-4=2(x+2)(mex-1)
因φ(0)≥0,则m≥1
令φ'(x)=0得x1=-lnm,x2=-2…(6分)
(1)若1≤m<e2,则-2<x1≤0,从而x∈(-2,x1)时φ'(x)<0;当x∈(x1,+∞)时φ'(x)>0,即φ(x)在 (-2,x1)单调递减,在(x1,+∞)单调递增,故φ(x)在[-2,+∞)的最小值φ(x1),φ(x1)=2mex1(x1+1)-
| x | 2 1 |
| x | 2 1 |
| x | 2 1 |
故当x≥-2时φ(x)≥0,即mg(x)≥f'(x)+2恒成立. …(8分)
(2)若m=e2,则φ'(x)=2e2(x+2)(ex-e-2),从而当x≥-2时φ'(x)≥0,即φ(x)在[-2,+∞)单调递增,而φ(-2)=0,故当x≥-2时φ(x)≥0,即mg(x)≥f'(x)+2恒成立.
(3)若m>e2,则φ(-2)=-2me-2+2=-2e-2(m-e2)<0,从而当x≥-2时,mg(x)≥f'(x)+2不可能恒成立. …(11分)
综上:m的取值范围是[1,e2]…(12分)
点评:此题主要考查利用导数研究曲线上某点切线方程,函数恒成立问题,考查分类讨论思想,解题的关键是能够利用导数工具研究函数的性质,此题是一道中档题.

练习册系列答案
相关题目
给出下列图象,其中可能为函数f(x)=x4+ax3+cx+d(a,b,c,d∈R)的图象是( )
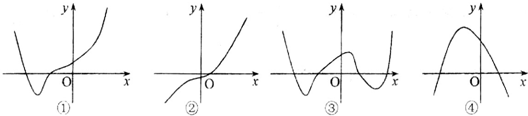

| A、①③ | B、①② | C、③④ | D、②④ |
函数f(x)=
+lg(1-x)的定义域是( )
| 1 |
| 1-x |
| A、(-1,1)∪(1,+∞) |
| B、(1,+∞) |
| C、(-∞,1) |
| D、(-∞,+∞) |
在△ABC中,角A,B,C,的对边分别为a,b,c,若(a2+c2-b2)tanB=
ac,则角B的值为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|