题目内容
如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:用定积分计算阴影部分的面积,利用几何概型的概率公式求出概率.
解答:
解:由题意,y=lnx与y=ex关于y=x对称,
∴阴影部分的面积为2
(e-ex)dx=2(ex-ex)
=2,
∵边长为e(e为自然对数的底数)的正方形的面积为e2,
∴落到阴影部分的概率为
.
故选:C.
∴阴影部分的面积为2
| ∫ | 1 0 |
| | | 1 0 |
∵边长为e(e为自然对数的底数)的正方形的面积为e2,
∴落到阴影部分的概率为
| 2 |
| e2 |
故选:C.
点评:本题考查几何概型,几何概型的概率的值是通过长度、面积、和体积的比值得到.

练习册系列答案
相关题目
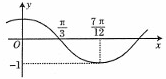 函数f(x)=sin(ωx+φ)({其中ω>0,|φ|<
函数f(x)=sin(ωx+φ)({其中ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知直线ax-by-2=0与曲线f(x)=x3在点P(1,f(1))处的切线互相垂直,则
=( )
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知函数y=
图象的对称中心为(2,-1),则a、b的值是( )
| bx-ab+1 |
| x-a |
| A、a=-2,b=-1 |
| B、a=-2,b=1 |
| C、a=2,b=1 |
| D、a=2,b=-1 |
若
、
、
三个单位向量两两之间夹角为60°,则|
+
+
|=( )
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| A、3 | ||
B、
| ||
| C、6 | ||
D、
|
等比数列{an}的各项为正数,且a5a6+a4a7=8,则log2a1+log2a2+…+log2a10=( )
| A、2+log25 |
| B、8 |
| C、10 |
| D、20 |