题目内容
某市有10 000名学生，一次信息技术成绩近似服从于正态分布N（70，100），如果规定不低于90分为优秀，那么成绩优秀的学生约为 人．（参考数据：P（μ-σ＜X＜μ+σ）=0.6828，P（μ-2σ＜X＜μ+2σ）=0.9544）
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：先由题意得：μ=70，σ=10．再利用正态分布的意义和3σ原则，即可得出结论．
解答：
解：因为由题意得：μ=70，σ=10，
所以P（70-20＜ξ＜70+20）=0.9544
所以P（ξ＞90）=
（1-0.9544）=2.28%．
所以成绩优秀的学生约为2.28%×10 000=228．
故答案为：228．
所以P（70-20＜ξ＜70+20）=0.9544
所以P（ξ＞90）=
| 1 |
| 2 |
所以成绩优秀的学生约为2.28%×10 000=228．
故答案为：228．
点评：本题主要考查了布正态分布的意义和应用，正态分布曲线的对称性，转化化归的思想方法，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
要得到函数y=-sin2x+
的图象，只需将y=sinxcosx的图象（ ）
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
设f1（x）=cosx，定义fn+1（x）为fn（x）的导数，即fn+1（x）=fn′（x），n∈N+，若△ABC的内角A满足f1（A）+f2（A）+…+f2014（A）=0，则sinA的值是（ ）
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
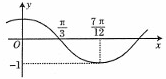函数f（x）=sin（ωx+φ）（{其中ω＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|