题目内容
（理）若函数f（x）=
，又记：f1（x）=f（x），fk+1（x）=f（fk（x）），k=1，2，3，…，则f2014（1）= ．
| x | ||
|
考点：函数的值
专题：函数的性质及应用
分析：根据条件求出fn（x）=
是表达式，然后直接代入求值即可．
| x | ||
|
解答：
解：∵f（x）=
，
∴f1（x）=f（x），f2（x）=f（f1（x））=
=
=
，
f3（x）=f（f2（x））=
，
则由归纳推理可得fn（x）=
，
即f2014（1）=
=
，
故答案为：
．
| x | ||
|
∴f1（x）=f（x），f2（x）=f（f1（x））=
| ||||||
|
| ||||||
|
| x | ||
|
f3（x）=f（f2（x））=
| x | ||
|
则由归纳推理可得fn（x）=
| x | ||
|
即f2014（1）=
| 1 | ||
|
| 1 | ||
|
故答案为：
| 1 | ||
|
点评：本题主要考查函数值的计算，利用条件求出函数fn（x）的表达式是解决本题的关键．
练习册系列答案
相关题目
在（x-
）5的展开式中x3的系数等于-5，则该展开式项的系数中最大值为（ ）
| a |
| x |
| A、5 | B、10 | C、15 | D、20 |
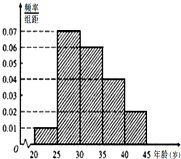近年来，我国许多省市雾霾天气频发，为增强市民的环境保护意识，某市面向全市征召N名义务宣传志愿者，成立环境保护宣传组织．现把该组织的成员按年龄分成5组：第1组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45]，得到的频率分布直方图如图所示，已知第2组有35人．
如图，有一个形如六边形的点阵，它的中心是一个点（算第1层），第2层每边有两个点，第3层每边有三个点，依此类推．如果一个六边形点阵共有169个点，那么它一共有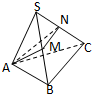
如图，三棱锥S-ABC中，SA=AB=AC=2，∠ASB=∠BSC=∠CSA=30°，M、N分别为SB、SC上的点，则△AMN周长最小值为