题目内容
已知椭圆C:
+
=1(a>b>0)的两焦点与短轴的一个端点的连线构成等腰直角三角形,且直线x-y+b=0是抛物线y2=4x的一条切线.
(1)求椭圆C的方程.
(2)过点S(0,-
)且斜率为1的直线l交椭圆C于M,N两点,求△OMN的面积.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程.
(2)过点S(0,-
| 1 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)直线代入抛物线方程,利用直线x-y+b=0与抛物线y2=4x相切,可得△=(2b-4)2-4b2=0,求出b,再利用椭圆
+
=1(a>b>0)的两焦点与短轴的一个端点的连线构成等腰直角三角形,求出a,即可求椭圆C的方程;
(2)直线l的方程为y=x-
,与
+y2=1联立消y,求出|MN|及原点O到直线l的距离,即可求△OMN的面积.
| x2 |
| a2 |
| y2 |
| b2 |
(2)直线l的方程为y=x-
| 1 |
| 2 |
| x2 |
| 2 |
解答:
解:(1)由
⇒x2+(2b-4)x+b2=0.
∵直线x-y+b=0与抛物线y2=4x相切,
∴△=(2b-4)2-4b2=0⇒b=1.
∵椭圆
+
=1(a>b>0)的两焦点与短轴的一个端点的连线构成等腰直角三角形,
∴a=
,
∴所求椭圆方程为
+y2=1.
(2)由已知得直线l的方程为y=x-
,与
+y2=1联立消y得3x2-2x-
=0.
设M(x1,y1),N(x2,y2),则x1+x2=
,x1•x2=-
,
∴(y1-y2)2=(x1-x2)2=(x1+x2)2-4x1x2=
,
∴|MN|=
=
.
又原点O到直线l的距离为d=
,
∴S△OMN=
×
×
=
.
|
∵直线x-y+b=0与抛物线y2=4x相切,
∴△=(2b-4)2-4b2=0⇒b=1.
∵椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴a=
| 2 |
∴所求椭圆方程为
| x2 |
| 2 |
(2)由已知得直线l的方程为y=x-
| 1 |
| 2 |
| x2 |
| 2 |
| 3 |
| 2 |
设M(x1,y1),N(x2,y2),则x1+x2=
| 2 |
| 3 |
| 1 |
| 2 |
∴(y1-y2)2=(x1-x2)2=(x1+x2)2-4x1x2=
| 22 |
| 9 |
∴|MN|=
| (x1-x2)2+(y1-y2)2 |
2
| ||
| 3 |
又原点O到直线l的距离为d=
| 1 | ||
2
|
∴S△OMN=
| 1 |
| 2 |
2
| ||
| 3 |
| 1 | ||
2
|
| ||
| 2 |
点评:本题考查直线与抛物线的位置关系,考查椭圆的方程,考查直线与椭圆的位置关系,考查三角形面积的计算,正确运用韦达定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果loga8>logb8>0,那么a、b间的关系是( )
| A、0<a<b<1 |
| B、1<a<b |
| C、0<b<a<1 |
| D、1<b<a |
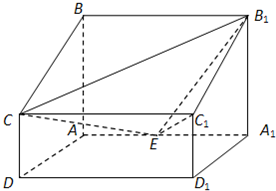 四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为AA1的中点.
四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为AA1的中点.