题目内容
设m、n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①若m⊥α,n∥α,则m⊥n
②若α∥β,β∥γ,m⊥α,则m⊥γ
③若m∥α,m∥β,α∩β=n,则m∥n
④若α⊥γ,β⊥γ,α∩β=m,则m⊥γ.正确命题的个数是( )
①若m⊥α,n∥α,则m⊥n
②若α∥β,β∥γ,m⊥α,则m⊥γ
③若m∥α,m∥β,α∩β=n,则m∥n
④若α⊥γ,β⊥γ,α∩β=m,则m⊥γ.正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:空间中直线与平面之间的位置关系
专题:开放型,空间位置关系与距离
分析:设m∩α=O,过O与直线n的平面β,利用线面平行的性质得线线平行,再由线线平行得线线垂直,来判断①是否正确;根据平行平面中的一个垂直于一条直线,另一个也垂直于这条直线,由此判断②是否正确;利用线面平行的性质与判定,即可判断;过m上任意一点作γ的垂线a,利用面面垂直的性质,可得结论.
解答:
解:①设m∩α=O,过O与直线n的平面β,α∩β=a,∵n∥α,∴a∥n,又m⊥α,∴m⊥a,∴m⊥n,故①是真命题;
②∵α∥β,m⊥α,∴m⊥β,β∥γ,∴m⊥γ,故②是真命题;
③设经过m的平面与α相交于b,则∵m∥α,∴m∥b,同理设经过m的平面与β相交于c,∵m∥β,∴m∥c,∴b∥c,∴b∥β,∵α∩β=n,∴b∥n,∴m∥n,故③是真命题;
④若α⊥γ,β⊥γ,α∩β=m,过m上任意一点作γ的垂线a,利用面面垂直的性质,可知a既在α内,又在β内,∴a与m重合,则m⊥γ,故④是真命题.
故选:D.
②∵α∥β,m⊥α,∴m⊥β,β∥γ,∴m⊥γ,故②是真命题;
③设经过m的平面与α相交于b,则∵m∥α,∴m∥b,同理设经过m的平面与β相交于c,∵m∥β,∴m∥c,∴b∥c,∴b∥β,∵α∩β=n,∴b∥n,∴m∥n,故③是真命题;
④若α⊥γ,β⊥γ,α∩β=m,过m上任意一点作γ的垂线a,利用面面垂直的性质,可知a既在α内,又在β内,∴a与m重合,则m⊥γ,故④是真命题.
故选:D.
点评:本题考查了线线、线面的位置关系,考查了学生的空间想象能力,解题的关键是熟练掌握线面垂直的判定定理与性质定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一个正三棱柱的每一条棱长都是a,则经过底面一边和相对侧棱的一个端点的截面(即图中△ACD)的面积为( )
一个正三棱柱的每一条棱长都是a,则经过底面一边和相对侧棱的一个端点的截面(即图中△ACD)的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知|
|=1,|
|=2且(
+
)与
垂直,则
与
的夹角是( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、60° | B、90° |
| C、135° | D、120° |
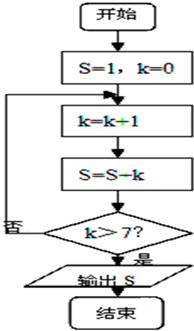 执行如图所示的程序框图,则输出的结果是( )
执行如图所示的程序框图,则输出的结果是( )| A、28 | B、29 | C、36 | D、37 |
已知一元二次不等式f(x)≤0的解集为{x|x≤
,或x≥3},则f(ex)>0的解集为( )
| 1 |
| 2 |
| A、{x|x<-ln2,或x>ln3} |
| B、{x|ln2<x<ln3} |
| C、{x|x<ln3}} |
| D、{x|-ln2<x<ln3} |
 如图,在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,点E、F、G分别是各自所在棱的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,点E、F、G分别是各自所在棱的中点.