题目内容
把命题“?x0∈R，x02-2x0+1＜0”的否定写在横线上 ．
考点：命题的否定
专题：简易逻辑
分析：利用特称命题的否定是全称命题写出结果即可．
解答：
解：特称命题的否定是全称命题
∴命题“?x0∈R，x02-2x0+1＜0”的否定是：?x∈R，x2-2x+1≥0．
故答案为：?x∈R，x2-2x+1≥0．
∴命题“?x0∈R，x02-2x0+1＜0”的否定是：?x∈R，x2-2x+1≥0．
故答案为：?x∈R，x2-2x+1≥0．
点评：本题考查命题的否定，全称命题与特称命题的否定关系，考查基本知识的应用．
练习册系列答案
相关题目
设正项等比数列{an}的前n项和为Sn，公比为q，若Sk-2=3，Sk=15，Sk+2=63，则q=（ ）
| A、-2 | B、2 | C、-4 | D、4 |
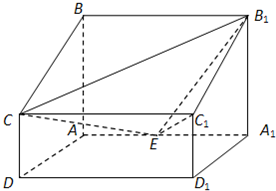四棱柱ABCD-A1B1C1D1中，AA1⊥底面ABCD，AB∥CD，AB⊥AD，AD=CD=1，AA1=AB=2，E为AA1的中点．
已知|
|=1，|
|=2且（
+
）与
垂直，则
与
的夹角是（ ）
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、60° | B、90° |
| C、135° | D、120° |