题目内容
 如图,有一个形如六边形的点阵,它的中心是一个点(算第1层),第2层每边有两个点,第3层每边有三个点,依此类推.如果一个六边形点阵共有169个点,那么它一共有
如图,有一个形如六边形的点阵,它的中心是一个点(算第1层),第2层每边有两个点,第3层每边有三个点,依此类推.如果一个六边形点阵共有169个点,那么它一共有考点:归纳推理
专题:常规题型
分析:先根据条件对每一层的点的个数进行列举,然后通过归纳推理,得到各层的点的个数的一个规律,再利用这个规律求出共有n层时点的总数,结合条件,求出图形的层数.
解答:
解:第一层有点数为:1,
第二层有点数为:6,
第三层有点数为:(顶点+边的中点)6+6=2×6,
第四层有点的个数为:(在第三层基础上,各边多一点)6+6+6=3×6,
第五层有点的个数为:(在第四层基础上,各边多一点)6+6+6+6=4×6,
…
∴第n(n≥2,n∈N*)层有点的个数为:(在第n-1层基础上,各边多一点)6(n-1).
设一个图形共有n(n≥2,n∈N*)层时,共有的点数为:
1+6+6+…+6(n-1)=1+
×n=3n2-3n+1
由题意得:3n2-3n+1=169,
∴(n+7)(n-8)=0.
∵n≥2,n∈N*
∴n=8.
故一共有8层.
故答案为:8.
第二层有点数为:6,
第三层有点数为:(顶点+边的中点)6+6=2×6,
第四层有点的个数为:(在第三层基础上,各边多一点)6+6+6=3×6,
第五层有点的个数为:(在第四层基础上,各边多一点)6+6+6+6=4×6,
…
∴第n(n≥2,n∈N*)层有点的个数为:(在第n-1层基础上,各边多一点)6(n-1).
设一个图形共有n(n≥2,n∈N*)层时,共有的点数为:
1+6+6+…+6(n-1)=1+
| 6+6(n-1) |
| 2 |
由题意得:3n2-3n+1=169,
∴(n+7)(n-8)=0.
∵n≥2,n∈N*
∴n=8.
故一共有8层.
故答案为:8.
点评:本题考查了归纳推理知识,要求先列举,后归纳,再应用.解题的关键在于归纳出各层点数的规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知三点A(2,1),B(1,-2),C(
,-
),动点P(a,b)满足0≤
•
≤2,且0≤
•
≤2,则动点P到点C的距离小于
的概率为( )
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 5 |
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
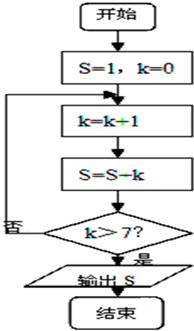 执行如图所示的程序框图,则输出的结果是( )
执行如图所示的程序框图,则输出的结果是( )| A、28 | B、29 | C、36 | D、37 |
 已知椭圆E:
已知椭圆E: