题目内容
2．
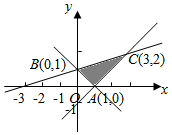设x，y满足如图所示的可行域（阴影部分），则$z=\frac{1}{2}x-y$的最大值为（ ）| A． | $\frac{1}{2}$ | B． | 0 | C． | $-\frac{1}{2}$ | D． | -1 |
分析 把目标函数化为y=$\frac{1}{2}$x-z，平移直线y=$\frac{1}{2}$x-z找出最优解，求出目标函数的最大值．
解答 
解：x，y满足如图所示的可行域（阴影部分），
则目标函数$z=\frac{1}{2}x-y$可化为y=$\frac{1}{2}$x-z，
平移直线y=$\frac{1}{2}$x-z，
当直线y=$\frac{1}{2}$x-z过点A（1，0）时，
z取得最大值为zmax=$\frac{1}{2}$×1-0=$\frac{1}{2}$．
故选：A．
点评 本题考查了简单的线性规划的应用问题，是基础题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
13．已知函数y=f（x）的图象关于y轴对称，当x∈（0，+∞）时，f（x）=log2x，若a=f（-3），b=f（$\frac{1}{4}$），c=f（2），则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞a＞b | D． | a＞c＞b |