题目内容
不等式|x+1|(2x-1)≥0的解集是( )
A、[
| ||
B、(-∞,-1]∪[
| ||
C、{-1}∪[
| ||
D、[-1,-
|
考点:其他不等式的解法
专题:不等式的解法及应用
分析:利用|x+1|≥0,原不等式等价为|x+1|=0或2x-1≥0,解之即可.
解答:
解:因为|x+1|≥0,所以不等式|x+1|(2x-1)≥0可化为|x+1|=0或2x-1≥0,解得x=-1或x≥-
,
则不等式|x+1|(2x-1)≥0的解集是{-1}∪[
,+∞).
故选:C.
| 1 |
| 2 |
则不等式|x+1|(2x-1)≥0的解集是{-1}∪[
| 1 |
| 2 |
故选:C.
点评:本题考查绝对值的意义,不等式的解法,等价转化.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若有一段演绎推理:“大前提:对任意实数a,都有(
)n=a.小前提:已知a=-2为实数.结论:(
)4=-2.”这个结论显然错误,是因为( )
| n | a |
| 4 | -2 |
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |
已知函数y=Asin(ωx+φ)在同一周期内,当x=
时,取得最大值y=3,当x=
时,取得最小值y=-3,则函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=3sin(2x-
| ||||
B、y=3sin(
| ||||
C、y=3sin(2x+
| ||||
D、y=3sin(2x+
|
若数列{xn}满足lgxn+1=1+lgxn,且x1+x2+…+x100=100,则lg(x101+x102+…+x200)=( )
| A、102 | B、100 |
| C、1000 | D、101 |
在△ABC中,A=60°,b=1,c=4,则△ABC外接圆的直径为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
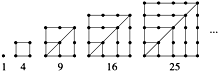 我们把1,4,9,16,25,…这些数称做正方形数,这是因为这些数目的点子可以排成一个正方形(如图).试求第n个正方形数是( )
我们把1,4,9,16,25,…这些数称做正方形数,这是因为这些数目的点子可以排成一个正方形(如图).试求第n个正方形数是( )| A、n(n-1) |
| B、n(n+1) |
| C、n2 |
| D、(n+1)2 |