题目内容
已知等差数列{an}的前n项和为Sn=n2+pn+q(p,q∈R),且a2,a3,a5成等比数列.
(1)求p,q的值;
(2)若数列{bn}满足an+log2n=log2bn,求数列{bn}的前n项和Tn.
(1)求p,q的值;
(2)若数列{bn}满足an+log2n=log2bn,求数列{bn}的前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:解法一:
(1)a1=S1=1+p+q,an=Sn-Sn-1=2n-1+p,由此求出q=0,由a2,a3,a5成等比数列,得p=-1.
(2)an=2n-2,bn=n•2an=n•22n-2=n•4n-1,由此利用错位相减法能求出数列{bn}的前n项和Tn.解法二:
(1)由Sn=n2+pn+q,得d=2,p=a1-1,q=0.由a2,a3,a5成等比数列,得p=-1.
(2)an=2n-2.bn=n•2an=n•22n-2=n•4n-1,由x+x2+x3+…+xn=
(x≠1),两边对x取导数得,由此能求出Tn=
[(3n-1)•4n+1].
(1)a1=S1=1+p+q,an=Sn-Sn-1=2n-1+p,由此求出q=0,由a2,a3,a5成等比数列,得p=-1.
(2)an=2n-2,bn=n•2an=n•22n-2=n•4n-1,由此利用错位相减法能求出数列{bn}的前n项和Tn.解法二:
(1)由Sn=n2+pn+q,得d=2,p=a1-1,q=0.由a2,a3,a5成等比数列,得p=-1.
(2)an=2n-2.bn=n•2an=n•22n-2=n•4n-1,由x+x2+x3+…+xn=
| x-xn+1 |
| 1-x |
| 1 |
| 9 |
解答:
(本小题满分14分)
解法一:
(1)解:当n=1时,a1=S1=1+p+q,…(1分)
当n≥2时,an=Sn-Sn-1…(2分)
=n2+pn+q-[(n-1)2+p(n-1)+q]
=2n-1+p.…(3分)
∵{an}是等差数列,
∴1+p+q=2×1-1+p,得q=0.…(4分)
又a2=3+p,a3=5+p,a5=9+p,…(5分)
∵a2,a3,a5成等比数列,
∴
=a2
,即(5+p)2=(3+p)(9+p),…(6分)
解得p=-1.…(7分)
(2)解:由(1)得an=2n-2.…(8分)
∵an+log2n=log2bn,
∴bn=n•2an=n•22n-2=n•4n-1.…(9分)
∴Tn=b1+b2+b3+…+bn-1+bn
=40+2×41+3×42+…+(n-1)•4n-2+n•4n-1,①…(10分)
4Tn=41+2×42+3×43+…+(n-1)•4n-1+n•4n,②…(11分)
①-②得-3Tn=40+41+42+…+4n-1-n•4n=
-n•4n=
.…(13分)
∴Tn=
[(3n-1)•4n+1].…(14分)
解法二:
(1)解:设等差数列{an}的公差为d,
则Sn=na1+
d=
n2+(a1-
)n.…(1分)
∵Sn=n2+pn+q,
∴
=1,a1-
=p,q=0.…(4分)
∴d=2,p=a1-1,q=0.
∵a2,a3,a5成等比数列,
∴
=a2
,…(5分)
即(a1+4)2=(a1+2)(a1+8).
解得a1=0.…(6分)
∴p=-1.…(7分)
(2)解:由(1)得an=2n-2.…(8分)
∵an+log2n=log2bn,
∴bn=n•2an=n•22n-2=n•4n-1.…(9分)
∴Tn=b1+b2+b3+…+bn-1+bn
=40+2×41+3×42+…+(n-1)•4n-2+n•4n-1.…(10分)
由x+x2+x3+…+xn=
(x≠1),…(11分)
两边对x取导数得,
x0+2x1+3x2+…+nxn-1=
.…(12分)
令x=4,得40+2×41+3×42+…+(n-1)•4n-2+n•4n-1=
[(3n-1)•4n+1].
∴Tn=
[(3n-1)•4n+1].…(14分)
解法一:
(1)解:当n=1时,a1=S1=1+p+q,…(1分)
当n≥2时,an=Sn-Sn-1…(2分)
=n2+pn+q-[(n-1)2+p(n-1)+q]
=2n-1+p.…(3分)
∵{an}是等差数列,
∴1+p+q=2×1-1+p,得q=0.…(4分)
又a2=3+p,a3=5+p,a5=9+p,…(5分)
∵a2,a3,a5成等比数列,
∴
| a | 2 3 |
| a | 5 |
解得p=-1.…(7分)
(2)解:由(1)得an=2n-2.…(8分)
∵an+log2n=log2bn,
∴bn=n•2an=n•22n-2=n•4n-1.…(9分)
∴Tn=b1+b2+b3+…+bn-1+bn
=40+2×41+3×42+…+(n-1)•4n-2+n•4n-1,①…(10分)
4Tn=41+2×42+3×43+…+(n-1)•4n-1+n•4n,②…(11分)
①-②得-3Tn=40+41+42+…+4n-1-n•4n=
| 1-4n |
| 1-4 |
| (1-3n)•4n-1 |
| 3 |
∴Tn=
| 1 |
| 9 |
解法二:
(1)解:设等差数列{an}的公差为d,
则Sn=na1+
| n(n-1) |
| 2 |
| d |
| 2 |
| d |
| 2 |
∵Sn=n2+pn+q,
∴
| d |
| 2 |
| d |
| 2 |
∴d=2,p=a1-1,q=0.
∵a2,a3,a5成等比数列,
∴
| a | 2 3 |
| a | 5 |
即(a1+4)2=(a1+2)(a1+8).
解得a1=0.…(6分)
∴p=-1.…(7分)
(2)解:由(1)得an=2n-2.…(8分)
∵an+log2n=log2bn,
∴bn=n•2an=n•22n-2=n•4n-1.…(9分)
∴Tn=b1+b2+b3+…+bn-1+bn
=40+2×41+3×42+…+(n-1)•4n-2+n•4n-1.…(10分)
由x+x2+x3+…+xn=
| x-xn+1 |
| 1-x |
两边对x取导数得,
x0+2x1+3x2+…+nxn-1=
| nxn+1-(n+1)xn+1 |
| (1-x)2 |
令x=4,得40+2×41+3×42+…+(n-1)•4n-2+n•4n-1=
| 1 |
| 9 |
∴Tn=
| 1 |
| 9 |
点评:本题考查实数的求法,考查数列的前n项和的求法,解题时要注意审题,注意错位相减法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式|x+1|(2x-1)≥0的解集是( )
A、[
| ||
B、(-∞,-1]∪[
| ||
C、{-1}∪[
| ||
D、[-1,-
|
给出下列三个函数的图象:
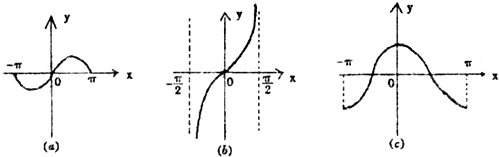
它们对应的函数表达式分别满足下列性质中的一条:
①f(2x)=2[f(x)]2-1
②f(x+y)=
③[f(2x)]2=4[f(x)]2(1-[f(x)]2)
则正确的对应方式是( )

它们对应的函数表达式分别满足下列性质中的一条:
①f(2x)=2[f(x)]2-1
②f(x+y)=
| f(x)+f(y) |
| 1-f(x)f(y) |
③[f(2x)]2=4[f(x)]2(1-[f(x)]2)
则正确的对应方式是( )
| A、(a)-①,(b)-②,(c)-③ |
| B、(b)-①,(c)-②,(a)-③ |
| C、(c)-①,(b)-②,(a)-③ |
| D、(a)-①,(c)-②,(b)-③ |
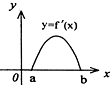 设f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )
设f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )